海洋学研究 >

2024 , Vol. 42 >Issue 2: 71 - 80

DOI: https://doi.org/10.3969/j.issn.1001-909X.2024.02.007

研究论文

海上移动平台GNSS可降水量反演影响因素研究

  • 曹凯 1, 2 ,
  • 罗孝文 1, 2, * ,
  • 文崧 2, 3 ,
  • 尤伟 2
展开
  • 1.山东科技大学 测绘与空间信息学院, 山东 青岛 266590
  • 2.自然资源部海底科学重点实验室,自然资源部第二海洋研究所,浙江 杭州 310012
  • 3.成都理工大学 沉积地质研究院,四川 成都 610059
*罗孝文(1972—),男,研究员,主要从事地球信息与探测技术方面的研究,E-mail: cdslxw@163.com。

曹凯(1999—),男,山东省临沂市人,主要从事GNSS数据处理方面的研究,E-mail: ck13791511873@163.com。

收稿日期: 2023-11-07

  修回日期: 2024-01-23

  网络出版日期: 2024-08-09

基金资助

国家重点研发计划项目(2022YFC3003800)

中央级公益性科研院所基本科研业务费专项资金资助项目(YJJC2401)

浙江省财政一般公共预算资助项目(330000210130313013006)

收起

Research on precipitable water vapor inversion influencing factors of GNSS for offshore mobile platforms

  • CAO Kai 1, 2 ,
  • LUO Xiaowen 1, 2, * ,
  • WEN Song 2, 3 ,
  • YOU Wei 2
Expand
  • 1. College of Geodesy and Geomatics, Shandong University of Science and Technology, Qingdao 266590, China
  • 2. Key Laboratory of Submarine Geosciences, Second Institute of Oceanography, MNR, Hangzhou 310012, China
  • 3. Institute of Sedimentary Geology, Chengdu University of Technology, Chengdu 610059, China

Received date: 2023-11-07

  Revised date: 2024-01-23

  Online published: 2024-08-09

Fold

摘要

基于海上移动平台GNSS动态精密单点定位技术(precise point positioning, PPP),对海洋上空可降水量(precipitable water vapor, PWV)探测的影响因素进行了研究,主要分析了采样间隔,卫星截止高度角,PPP解算方式(固定解或浮点解)以及有无北斗卫星系统组合对海洋PWV反演的影响。结果显示,采样间隔为30 s时,PWV反演的精度最高;可用卫星数较少的情况下,截止高度角设为5°~10°时,PWV反演精度更优,随着卫星截止高度角的增大,反演精度逐渐降低;定位解是否固定对PWV反演精度影响较小;在GPS/GLONASS系统组合的基础上,加入北斗卫星观测值,将提高观测的冗余度,有利于PWV反演精度的提高。

关键词： 海上移动平台; 精密单点定位技术(PPP); 北斗卫星(BDS); PWV; 影响因素

本文引用格式

曹凯 , 罗孝文 , 文崧 , 尤伟 . 海上移动平台GNSS可降水量反演影响因素研究[J]. 海洋学研究, 2024 , 42(2) : 71 -80 . DOI: 10.3969/j.issn.1001-909X.2024.02.007

Abstract

Based on Global Navigation Satellite System (GNSS) dynamic precision point positioning technology (PPP), the influence factors of precipitable water vapor (PWV) detection over the ocean were studied. The sampling interval, satellite masking angle, PPP solution method (fixed solution or floating point solution), and the influence of Beidou satellite system combination on ocean PWV retrieval were mainly analyzed. In the marine observation environment, the results show that the accuracy of PWV inversion is the highest when the sampling interval is 30 s. When the number of available satellites is small, the accuracy of PWV inversion is better when the satellite masking angle is set to 5°-10°, and the accuracy decreases gradually with the increase of the satellite masking angle. Whether the PPP solution is fixed or not, it has little effect on the accuracy of PWV inversion. On the basis of GPS/GLONASS system combination, adding Beidou observation value will improve the redundancy of observation and improve the accuracy of PWV inversion.

Key words： offshore mobile platform; precise point positioning (PPP); Beidou Navigation Satellite System (BDS); precipitable water vapor(PWV); influencing factors

0 引言

对流层中的可降水量(precipitable water vapor, PWV)是气象预测应用、气候变化研究和数值气象模型(numerical weather models, NWM)中的重要参数。已有不少研究将全球导航卫星系统(global navigation satellite system, GNSS)地基站反演的PWV与不同观测方式获取的PWV进行了对比分析,如无线电探空仪[1-2]、微波辐射计[3]、卫星测量[4]、Raman Lidar测量[5]等,对比精度大约为1~5 mm。随着全球各独立卫星导航系统的不断建设和完善,多种卫星导航系统的组合为实时高精度的PWV解算提供了更为有利的条件。海洋环境下,利用GNSS观测值获取PWV的精度与可靠性得到了显著提升。
CHADWELL等[6]发现在沿海地区,利用浮标记录的GPS数据可以直接用来估计PWV,用于天气预报、天基微波辐射计校准和气候研究。有研究证明了船载GPS在海上估计的PWV与无线电探空仪观测结果非常一致[7-8]。BONIFACE等[9]使用船载GNSS和NWM的组合来反演PWV,并与地中海上空的中分辨率成像光谱仪(MODIS)反演值进行了比较,结果证明两者之间没有明显的偏差。FAN等[10]在中国渤海利用GPS进行PWV反演估计,将反演的PWV与MM5模式(fifth-generation penn state/NCAR mesoscale model)积分的PWV进行比较,发现两者具有近乎相同的精度。SHOJI等[11]将船载GNSS反演的PWV与北太平洋西部和日本附近海域的无线电探空仪观测结果进行了比较,研究表明GNSS有助于监测海洋上空的PWV。SOHN等[12]利用无线电探空仪观测结果及美国国家航天航空局Aqua卫星输出的大气红外探测器(AIRS)观测值作为参考值进行对比研究,认为船载GNSS具有足够的潜力可以通过精密单点定位技术(precise point positioning, PPP)求解PWV。
上述各项研究利用船载或浮标搭载的GNSS估计PWV(GNSS-PWV),并与他们研究中描述的各参考值进行了比较分析,验证了GNSS-PWV的精度与可靠性,但很少有学者对海洋环境中影响PWV反演精度的因素进行研究分析。影响PWV反演精度的因素主要包括三部分:天顶对流层延迟的估计、干延迟的计算以及大气平均温度的确定。由于缺乏气象数据的支持,有关气象参数计算的部分采用精度已经得到验证的温度气象模型GPT3(Global Pressure and Temperature 3)[13-14]来进行补充,本文主要从天顶对流层延迟估计方面讨论PWV反演的影响因素。使用海上移动平台GNSS数据,按照不同的处理策略进行解算,讨论不同采样间隔、不同卫星截止高度角、不同PPP解算方式以及有无北斗卫星系统组合下的PWV反演值变化。将各方案的反演值与距离最近的探空站PWV值进行比较,由此评估不同处理策略的优劣,为后续的实时高精度PWV解算提供参考。

1 数据与方法

1.1 实验数据来源

海上移动平台GNSS数据观测时间为2021年4月—5月,共计61天。接收机类型为天宝Net-R9,采样率为30 s,导航文件和卫星事后精密轨道、钟差文件、DCB等产品下载自武汉大学IGS数据中心(www.igs.gnsswhu.cn/)。气象参数获取自先验温度气象模型GPT3[15]。无线电探空站数据由美国怀俄明大学大气科学系无线电探空仪档案馆提供(http://weather.uwyo.edu/upperair/bufrraob.shtml),每个无线电探空站每天在协调世界时(UTC)00:00:00和12:00:00进行两次观测。本文选择的无线电探空站与GNSS接收机距离约为46 km,高度差约为2 m,将把探空站积分PWV值作为参考值对海上移动平台GNSS反演的PWV值进行评价。

1.2 基于PPP技术获取对流层湿延迟

文中实验部分将利用PPP技术来获取天顶对流层总延迟(zenith total delay,ZTD),具体PPP处理策略见表1。由于结果文件的高程坐标使用的是以参考椭球面为基准面的高程系统,因此在进行实际计算时需要采用地球重力场模型EGM2008将结果高程数据改正为正常高。随后利用Saastamoinen模型计算天顶对流层干延迟 (zenith hydrostatic delay,ZHD)。其中,ZHD计算需要的气象参数由GPT3模型1°×1°格网产品计算得出,具体公式为
$\begin{array}{l} r(t)=A_{0}+A_{1} \cos \left(\frac{\mathrm{DOY}}{365.25} 2 \pi\right)+B_{1} \sin \left(\frac{\mathrm{DOY}}{365.25} 2 \pi\right)+ \\ A_{2} \cos \left(\frac{\mathrm{DOY}}{365.25} 4 \pi\right)+B_{2} \sin \left(\frac{\mathrm{DOY}}{365.25} 4 \pi\right) \end{array}$
式中:r(t)为格网处的气象参数值,DOY为年积日,A0为年平均振幅,A1、B1为年周期振幅,A2、B2为半年周期振幅。各个振幅值通过VMF3/GPT3官网给出的相关代码计算得到。最后采用双线性内插法获取测站处的气象参数。
表1 PPP处理策略汇总表

Tab.1 Summary table of PPP processing strategy

参数 策略
处理模式 动态处理
卫星观测系统 GPS、GLONASS、BDS
观测值类型 伪距和载波相位
频率 GPS/GLONASS(L1,L2),BDS(B1,B2)
卫星天线相位中心改正 igs14.atx
接收机天线相位中心改正 igs14.atx
海潮改正模型 FES2004.BLQ
映射函数 GMF
相位缠绕改正 模型改正
相对论效应 模型改正
卫星轨道和钟差 wum最终产品
接收机钟差 白噪声
电离层模型 Ionosphere-Free-LC
对流层模型 参数估计
滤波 扩展卡尔曼滤波
模糊度固定方法 浮点解/固定解
然后,根据公式(2)获取天顶对流层湿延迟(zenith wet delay,ZWD):
ZWD=ZTD-ZHD
为了获取更高精度的ZTD,本研究将采用双向滤波处理整天的数据[16-17],其中00:00:00时刻数据为前一天前向滤波的24时和当天后向滤波0时的平均值,12:00:00时刻数据同理计算。

1.3 利用GNSS数据计算PWV的方法

通过计算得到ZWD后,使用式(3)和式(4)[18]计算得到对应的PWV值:
PWV=Π×ZWD
$\Pi=\frac{10^{6}}{\rho_{\mathrm{w}} \frac{R}{m_{\mathrm{w}}}\left[\frac{k_{3}}{T_{\mathrm{m}}}+k_{2}-\frac{m_{\mathrm{w}}}{m_{\mathrm{d}}} \cdot k_{1}\right]}$
式中:Π为转换系数; ρw为液态水的密度,ρw=1×103 kg/m3;k1、k2、k3为大气折射率常数,k1=77.604 K/hPa,k2=70.4 K/hPa,k3=3.739×105 K/hPa;md为干大气摩尔质量,md=28.96 kg/kmol;mw为湿大气摩尔质量,mw=18.02 kg/kmol;R为普适气体常数,R=83.14 hPa·m3·K-1·kmol-1;Tm为大气加权平均温度,可由公式(5)计算得到:
Tm= ∫ h 0 ∞ ( e / T ) d h ∫ h 0 ∞ ( e / T 2 ) d h
式中:e为测站垂直路径上的水汽压,单位为hPa;h0为起始椭球高,h为积分处椭球高,单位为m; T为测站的温度,单位为K。
由于水汽垂直分布的不均匀性和随时间变化的复杂性,Tm的精确积分很难求得。因此本文采用统计方法推导出的全球线性回归公式来计算对应的Tm。该方法是将纬度分为12个区域,利用2011—2015年的Tm和Ts数据分别拟合对应的线性关系式。根据本研究区的范围,对应的计算公式[19]为
Tm=105.152 9+0.611 7Ts
式中:Ts为地表温度,单位为K。
根据探空站数据的计算结果,该区域的转换系数在0.164~0.165之间波动,实际计算时以0.164为准。

1.4 利用无线电探空资料计算PWV的方法

无线电探空技术通过测量大气廓线的气象参数来计算可降水量,其原理是利用探空气球观测大气对流层中各个高度上的比湿,然后对气压从地面到对流层顶进行垂直积分:
PWV= ∫ 0 p 0 q ρ w gdp
式中:PWV为可降水量,单位为mm;q为比湿,单位为g/kg;g为重力加速度,单位为m/s2;p0为地面气压,p为积分处气压,单位为hPa。
由于无法获取连续的比湿和气压数据,因此可降水量的实际计算方法是利用多层等压面上的比湿数据对气压进行离散积分的过程,具体公式如下:
PWV=- 1 ρ w g ∑ p 0 0 q -Δp
式中: q -和Δp分别为两个相邻等压面间的平均比湿和气压差。由于PWV主要集中在大气层底部(0~12 km),实际只需计算地面到200 hPa气压面之间的PWV即可[20]。
由于无线电探空站与实验测站并不在同一位置,为了进行对比评估,在匹配测站时除了设定两站间的水平和垂直距离限制,还需要对无线电探空站结果中的温度、相对湿度和气压进行高程方向的补偿,以得到测站处的近似结果[21]。需要注意的是,无线电探空仪在每次进行探测时获取的等压面层数各不相同,这导致了作为参考标准的探空站PWV精度在各个历元时刻并不统一。下面为了统一无线电探空资料计算PWV的精度,将只使用标准等压面上的比湿来代替该历元获取的所有等压面上的比湿积分求和,进行比较(图1)。
图1 利用不同压力层计算的PWV值的对比图(a)以及PWV差值统计图(b)

Fig.1 The comparison of PWV values calculated by different pressure layers (a) and the corresponding difference statistics (b)

从图1a中可以看出不同数据层积分得到的PWV值相关系数为0.93,证明两者之间具有很强的相关性。两者的互差集中在-2~2 mm周围,差值呈正态分布(图1b),两者的平均偏差为-1.16 mm,均方根误差为2.48 mm。以上数据表明,可以使用标准等压面数据代替所有等压面数据进行PWV反演,本文中选用标准等压面数据进行计算。

2 数据处理与结果分析

由于海上观测环境恶劣,会存在多种因素影响PWV的估计精度,本文选择从采样间隔、卫星截止高度角、PPP解算方式以及有无北斗卫星系统组合四个方面进行讨论与分析,观察哪一种处理策略有利于提高海上移动平台GNSS反演PWV的精度。实验对比时刻(历元)为DOY121~DOY182中每天的 0时和12时(GPS 时间),实验共122个历元。由于无线电探空仪实际探测过程大约为15 min,所以将对应的15 min内GNSS反演的可降水量取平均作为0时和12时的GNSS-PWV值。

2.1 不同采样间隔对PWV反演值的影响

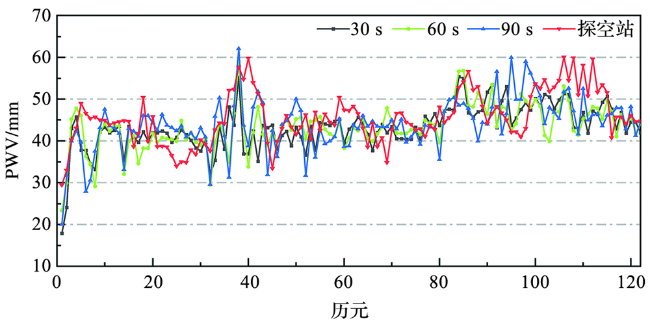
为分析不同的数据采样间隔对PWV的影响,设置了三种不同采样间隔,分别为30 s、60 s和90 s。使用GPS、GLONASS两个系统观测值参与计算,卫星截止高度角设置为10°,其余的PPP处理策略见表1。三种方案的实验结果对比和与探空站PWV差值的统计信息如图2和表2所示。
图2 不同采样间隔下的PWV反演值与探空站PWV计算值的对比

Fig.2 Comparison of PWV inversion values under different sampling intervals with those calculated from sounding radiosonde station

表2 不同采样间隔下的PWV反演值与探空站PWV计算值间的平均偏差及均方根误差统计

Tab.2 Statistics of the mean deviation and root mean square error between the PWV inversion values derived from different sampling intervals and those calculated from sounding radiosonde station

采样间隔/s 平均偏差/mm 均方根误差/mm
30 -2.36 6.34
60 -2.24 6.54
90 -1.72 7.10
从图中可以看出三种方案给出的PWV反演值的整体变化趋势基本相同,只有部分历元对应的PWV出现了较为明显的变化。其中,30 s和60 s方案的PWV反演值吻合程度较好,而90 s方案的PWV反演值在部分历元差异较大。与探空站PWV比较时,90 s方案的PWV反演值偏差较大的情况更为明显,这使其系统误差得以减小,但均方根误差较大,不够稳定。从表2中能够看出,均方根误差随着采样间隔的增大而增大。
从统计信息(表2)可以看出,30 s方案的精度最高,60 s方案其次,但精度与前者相差不大,90 s方案的精度最差。总体而言,采样间隔的改变(30~90 s内)对PWV反演存在一定的影响。随着数据采样间隔的减小,精度随之提高。但在保证PWV反演精度的前提下,适当提高数据的采样间隔可以显著减少数据存储空间和处理时间。

2.2 不同卫星截止高度角对PWV反演值的影响

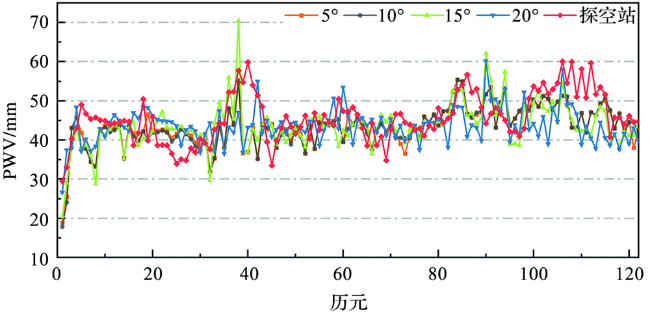
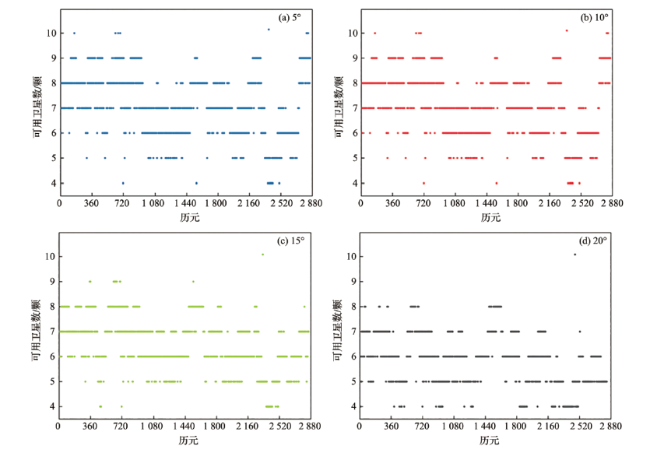
卫星截止高度角是GNSS数据处理中的重要指标,使用该指标可以对参与解算的观测值进行筛选。低卫星截止高度角的观测值中含有更多的对流层延迟信息,有利于PWV信息的提取,但同时也存在映射函数误差较大、卫星观测质量不佳等问题[22-23]。本节中数据采样间隔设置为30 s,使用GPS/GLONASS系统组合观测值参与计算,卫星截止高度角设置为5°、10°、15°和20°,其余的PPP处理策略见表1。四种方案的PWV反演值以及与探空站PWV值的对比结果与统计信息如图3和表3所示。
图3 不同卫星截止高度角下的PWV反演值与探空站PWV计算值的对比

Fig.3 Comparison of PWV inversion values under different satellite masking angles with those calculated from sounding radiosonde station

表3 不同卫星截止高度角下的PWV反演值与探空站PWV计算值间的平均偏差及均方根误差统计

Tab.3 Statistics of the mean deviation and root mean square error between the PWV inversion values obtained under different satellite masking angles and those calculated from sounding radiosonde station

卫星截止高度角/(°) 平均偏差/mm 均方根误差/mm
5 -2.08 6.38
10 -2.36 6.34
15 -2.90 7.26
20 -3.42 7.53
从图中可以看出四种方案的反演值与探空站结果的变化趋势基本一致,其中,5°和10°方案反演的PWV值近乎相同,15°和20°方案在某些历元时刻上与其他两个方案有些差别,特别是在50~70历元、100~120历元左右。其原因可以结合图4看出,图4是以4月30日单天为例的卫星可用数量变化。卫星截止高度角从5°增加到10°,卫星可用数量没有发生明显变化,因此参与计算的卫星可能也没有发生改变。而15°和20°的方案由于截止高度角的不断升高,导致部分历元出现可用卫星数变化剧烈,PPP过程重新收敛的情况,这一情况在整天的数据处理中会或多或少地影响到0时刻和12时刻的PWV反演精度。
图4 不同卫星截止高度角处理策略下的卫星可用数

Fig.4 The valid number of satellites under different satellite masking angle processing strategies

从表3统计结果来看,卫星截止高度角设为5°和10°时,精度最优。随着卫星截止高度角的增大,PWV反演精度逐渐降低。同时,由于海洋观测环境的复杂性,选择相对较低的卫星截止高度角,也可以保证拥有足够的可用卫星参与计算。

2.3 PPP解算模式对PWV反演值的影响

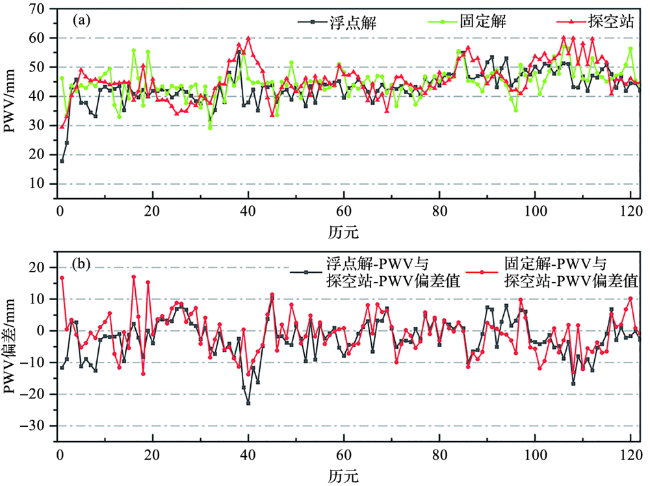
在精密单点定位解算ZTD时,可以选择不固定模糊度(浮点解)或固定模糊度(固定解),为了讨论浮点解和固定解对PWV反演的影响,本节实验将卫星截止高度角设置为10°,使用GPS/GLONASS系统组合参与计算,其余的PPP处理策略见表1。浮点解与固定解反演的PWV值与探空站结果的对比结果与统计信息如图5和表4所示。
图5 不同PPP解算方式反演的PWV值与探空站PWV计算值的对比

Fig.5 Comparison of PWV inversion values derived from different PPP processing methods with those calculated from sounding radiosonde station

表4 不同PPP解算方式以及不同卫星组合反演的PWV与探空站PWV计算值间的平均偏差及均方根误差统计

Tab.4 Statistics of the mean deviation and root mean square error between the PWV inverted from different PPP processing methods and satellite combinations, and those calculated from sounding radiosonde station

方法 平均偏差/mm 均方根误差/mm
浮点解(GPS/GLONASS) -2.36 6.34
固定解(GPS/GLONASS) -0.71 6.27
固定解(GPS/GLONASS/BDS) 0.23 5.20
从图5a和表4中可以看出,浮点解与固定解反演PWV的整体变化趋势与探空站结果较为一致。从两种方案反演值与探空站结果的差值来看(图5b),固定解相比于浮点解并没有明显的优势,均方根误差也相差无几(表4)。甚至在部分历元时刻,两者的反演值近乎相同。猜测是海上观测环境的不确定性,导致卫星可用数量变化剧烈,从而使固定解变得断断续续,选用固定解策略解算的部分历元值可能也存在浮点解没有固定的情况,甚至固定解在某些历元时刻和探空站PWV的差值变得更大了,不排除是模糊度错误固定的原因。综上所述,PPP解算模式的选择对PWV反演影响不大,这与陈冠旭等[24]的研究结论一致。但若海洋观测环境处在恶劣情况下,模糊度难以有效固定,仅考虑PWV反演精度而非定位精度,或许浮点解的适用性更强[25]。

2.4 北斗系统对PWV反演值的影响

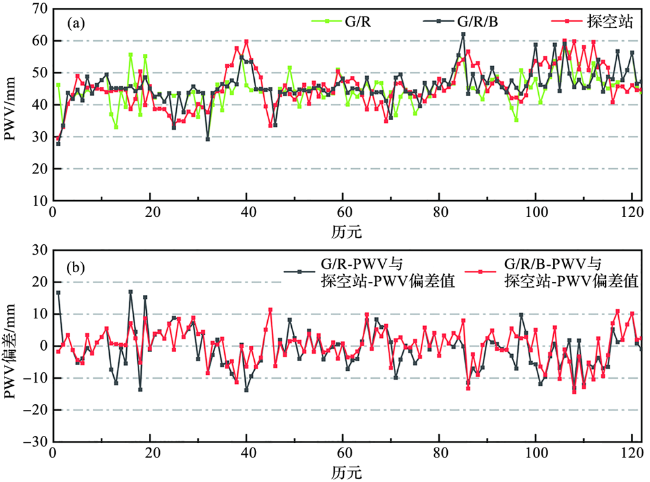
目前,PWV的估算多采用GPS系统,但随着北斗卫星系统(BDS)近些年的快速发展,在轨导航卫星数越来越多,可参与PWV计算的卫星资源变得更加丰富,且拥有较好的兼容性。为此,本文在GPS/GLONASS卫星系统的组合上,加入了北斗卫星系统并分析其对PWV反演的影响。在固定解的处理模式下,分别采用GPS/GLONASS组合和GPS/GLONASS/BDS组合系统数据对PWV进行反演,其对比结果和统计信息如图6和表4所示。
图6 不同卫星组合反演的PWV值与探空站PWV计算值的对比

(图中G/R表示GPS/GLNOASS卫星系统的组合,G/R/B表示GPS/GLONASS/BDS卫星系统的组合。)

Fig.6 Comparison of PWV inversion values derived from different satellite constellation combinations with those calculated from sounding radiosonde station

(G/R represents the combination of GPS/GLONASS satellite systems, while G/R/B represents the combination of GPS/GLONASS/BDS satellite systems.)

从图6和表4中可以看出,加入北斗卫星系统后,GNSS反演的PWV值与探空站结果的差距有所减小。GPS/GLONASS/BDS组合相较于GPS/GLONASS组合,平均偏差和均方根误差均有减小,均方根误差降低了约1.07 mm,说明部分历元的北斗卫星信号质量强于原本参与计算的GPS/GLONASS系统的卫星信号,或者说卫星的几何构型更优。另外,从图4可以看出,虽然观测到的卫星数量众多,但经过软件数据质量控制处理后的可用卫星数量却不多,从中能够看出观测冗余度对于PWV反演的影响也很大。在海洋环境下,北斗卫星系统的加入或许能够改善单天模糊度重新收敛的情况,提高PWV的反演精度和稳定性。

3 结论

本文基于GPT3模型,利用海上移动平台GNSS接收机观测数据,从采样间隔、卫星截止高度角、PPP解算方式、卫星系统组合四个方面进行了研究,分析其对海上PWV反演精度的影响,得到以下结论。
1)采样间隔对PWV反演值有一定的影响,采样间隔为30 s时,PWV反演的精度最高。随着采样间隔的增加(30~90 s),PWV反演精度逐渐降低。但在保证精度的前提下,适当提高数据采样间隔可以减少存储空间和处理时间的压力。
2)受卫星可用数量的影响,GPS/GLONASS组合使用较低的卫星截止高度角能避免某些时刻出现没有足够数量的卫星参与定位计算的情况,而GPS/GLONASS/BDS组合可以改善这种状况,同时可以使一天内PWV的反演值变得更加稳定。同时5°~10°左右的卫星截止高度角处理策略比较适合海上动态PPP反演PWV。
3)从整体的数据来看, PPP解算模式的选择对PWV反演的影响并不显著。
综合考虑上述情况,在观测环境和观测设备受限的情况下,选择适合的处理策略才能获得更高的PWV反演精度。海上动态GNSS反演PWV受到的影响因素众多,实验中的反演值会出现一些无法解释的突变,未来还需要对海上PWV反演异常值产生的来源和筛选的标准做进一步的研究。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
WANG J H, ZHANG L Y. Systematic errors in global radiosonde precipitable water data from comparisons with ground-based GPS measurements[J]. Journal of Climate, 2008, 21(10): 2218-2238.

[2]
PERDIGUER-LÓPEZ R, BERNÉ-VALERO J L, GARRIDO-VILLÉN N. Application of GNSS methodologies to obtain precipitable water vapor (PWV) and its comparison with radiosonde data[J]. Multidisciplinary Digital Publishing Institute Proceedings, 2019, 19(1): 24.

[3]
FIONDA E, CADEDDU M, MATTIOLI V, et al. Intercom-parison of integrated water vapor measurements at high latitudes from co-located and near-located instruments[J]. Remote Sensing, 2019, 11(18): 2130.

[4]
HE J, LIU Z Z. Water vapor retrieval from MODIS NIR channels using ground-based GPS data[J]. IEEE Transac-tions on Geoscience and Remote Sensing, 2020, 58(5): 3726-3737.

[5]
BARNES J E, KAPLAN T, VÖMEL H, et al. NASA/Aura/Microwave Limb Sounder water vapor validation at Mauna Loa observatory by Raman lidar[J]. Journal of Geophysical Research: Atmospheres, 2008, 113(D15): D15S03.

[6]
CHADWELL C D, BOCK Y. Direct estimation of absolute precipitable water in oceanic regions by GPS tracking of a coastal buoy[J]. Geophysical Research Letters, 2001, 28(19): 3701-3704.

[7]
ROCKEN C, JOHNSONJ, VAN HOVE T, et al. Atmospheric water vapor and geoid measurements in the open ocean with GPS[J]. Geophysical Research Letters, 2005, 32(12):L12813.

[8]
FUJITA M, KIMURA F, YONEYAMA K, et al. Verification of precipitable water vapor estimated from shipborne GPS measurements[J]. Geophysical Research Letters, 2008, 35(13): L13803.

[9]
BONIFACE K, CHAMPOLLION C, CHERY J, et al. Potential of shipborne GPS atmospheric delay data for prediction of Mediterranean intense weather events[J]. Atmospheric Science Letters, 2012, 13(4): 250-256.

[10]
FAN S J, ZANG J F, PENG X Y, et al. Validation of atmospheric water vapor derived from ship-borne GPS measurements in the Chinese Bohai Sea[J]. Terrestrial, Atmospheric and Oceanic Sciences, 2016, 27(2): 213-220.

[11]
SHOJI Y, SATO K, YABUKI M, et al. Comparison of shipborne GNSS-derived precipitable water vapor with radiosonde in the western North Pacific and in the seas adjacent to Japan[J]. Earth, Planets and Space, 2017, 69(1): 153.

[12]
SOHN D H, CHOI B K, PARK Y, et al. Precipitable water vapor retrieval from shipborne GNSS observations on the Korean research vessel ISABU[J]. Sensors, 2020, 20(15): 4261.

[13]
綦子民, 屈小川, 赖山东, 等. GPT3模型在安徽地区的性能[J]. 大地测量与地球动力学, 2023, 43(5):481-486.

QI Z M, QU X C, LAI S D, et al. Performance of GPT3 model in Anhui Province[J]. Journal of Geodesy and Geodynamics, 2023, 43(5): 481-486.

[14]
王来顺, 刘建忠, 张寅宝. GPT3模型中国区域大气剖面应用精度分析[J]. 测绘工程, 2023, 32(1):21-29,36.

WANG L S, LIU J Z, ZHANG Y B. Analysis of application accuracy of GPT3 model in China’s regional atmospheric profile[J]. Engineering of Surveying and Mapping, 2023, 32(1): 21-29, 36.

[15]
LANDSKRON D, BÖHM J. VMF3/GPT3: refined discrete and empirical troposphere mapping functions[J]. Journal of Geodesy, 2018, 92(4): 349-360.

[16]
李黎, 刘彦, 王迅, 等. 不同时空条件下RTKLib与在线PPP解算系统的ZTD精度评估[J]. 大地测量与地球动力学, 2023, 43(1):12-17.

LI L, LIU Y, WANG X, et al. ZTD precision analysis of RTKLib and online PPP resolution systems under varied spatiotemporal conditions[J]. Journal of Geodesy and Geodynamics, 2023, 43(1): 12-17.

[17]
范士杰, 胡卓, 彭秀英, 等. GPS水汽反演的双向滤波结果分析[J]. 测绘科学, 2019, 44(12):179-183.

FAN S J, HU Z, PENG X Y, et al. Analysison the bilateral filtering results of GPS water vapor inversion[J]. Science of Surveying and Mapping, 2019, 44(12): 179-183.

[18]
郭敏, 张捍卫, 李鹏杰. 大气加权平均温度对GNSS PWV精度的影响分析[J]. 地球物理学进展, 2023, 38(4):1455-1465.

GUO M, ZHANG H W, LI P J. Influence of weighted average temperature on PWV accuracy[J]. Progress in Geophysics, 2023, 38(4): 1455-1465.

[19]
YAO Y B, ZHANG B, XU C Q, et al. Analysis of the global Tm-Ts correlation and establishment of the latitude-related linear model[J]. Chinese Science Bulletin, 2014, 59(19): 2340-2347.

[20]
王朝阳. 中国沿海GPS/GLONASS组合水汽反演关键技术与变化特征研究[D]. 青岛: 山东科技大学, 2018.

WANG Z Y. Study on key technologies and variation of water vapor retrieval with GPS/GLONASS in the coastal regions of china[D]. Qingdao: Shandong University of Science and Technology, 2018.

[21]
刘梦杰, 涂满红, 王洪, 等. 台站处北斗/GNSS实时大气水汽反演及试验分析[J]. 测绘科学, 2022, 47(11):25-31.

LIU M J, TU M H, WANG H, et al. Construction of in situ BDS/GNSS real-time precipitable water vapor retrieval and experiment analysis[J]. Science of Surveying and Mapping, 2022, 47(11): 25-31.

[22]
王朝阳, 卢勇夺, 邢喆, 等. 卫星截止高度角、对流层映射函数和海潮模型对南极GNSS精密定位的影响分析[J]. 大地测量与地球动力学, 2020, 40(12):1294-1298.

WANG Z Y, LU Y D, XING Z, et al. Research on influence of satellite cut-off elevation angle, tropospheric mapping function and ocean tide model on Antarctica GNSS PPP[J]. Journal of Geodesy and Geodynamics, 2020, 40(12): 1294-1298.

[23]
范士杰, 刘焱雄, 高兴国, 等. 海上动态GPS大气可降水量信息反演[J]. 中国石油大学学报:自然科学版, 2012, 36(3):84-87,92.

FAN S J, LIU Y X, GAO X G, et al. Retrieval method of marine kinematic GPS precipitable water vapor[J]. Journal of China University of Petroleum: Edition of Natural Science, 2012, 36(3): 84-87, 92.

[24]
陈冠旭, 刘焱雄, 柳响林, 等. 船载GNSS探测海洋水汽信息的影响因子分析[J]. 武汉大学学报:信息科学版, 2017, 42(2):270-276.

CHEN G X, LIU Y X, LIU X L, et al. Analysison influen-cing factors of ocean water vapor estimated from shipborne GNSS measurements[J]. Geomatics and Information Science of Wuhan University, 2017, 42(2): 270-276.

[25]
朱恒, 郑竹锦, 祝会忠, 等. GNSS多系统实时对流层延迟估计及影响因素分析[J]. 测绘科学, 2022, 47(5):18-25.

ZHU H, ZHENG Z J, ZHU H Z, et al. Multi-GNSS real-time troposphere delay estimation and its impact factors analyzing[J]. Science of Surveying and Mapping, 2022, 47(5): 18-25.

Options
文章导航

/

〈 〉