海洋学研究 >

2024 , Vol. 42 >Issue 3: 142 - 152

DOI: https://doi.org/10.3969/j.issn.1001-909X.2024.03.012

研究论文

基于数据-知识驱动的高精度海底地形绘制:以南海为例

  • 刘洋 , 1, 2 ,
  • 李三忠 , 1, 2, * ,
  • 邹卓延 1, 2 ,
  • 索艳慧 1, 2 ,
  • 孙毅 1, 2
展开
  • 1.中国海洋大学 海洋地球科学学院,深海圈层与地球系统教育部前沿科学中心,海底科学与探测技术教育部重点实验室,山东 青岛 266100
  • 2.崂山实验室 海洋矿产资源评价与探测技术功能实验室,山东 青岛 266237
*李三忠(1968—),男,教授,主要从事海底科学与地球系统动力学研究,E-mail:。

刘洋(1997—),男,湖北省阳新县人,主要从事海洋地质方面的研究,E-mail:。

收稿日期: 2023-09-27

  修回日期: 2024-05-22

  网络出版日期: 2024-11-25

基金资助

青岛海洋科学与技术试点国家实验室山东省专项经费项目(2022QNLM05032)

国家自然科学基金项目(42121005)

国家自然科学基金项目(91958214)

山东省自然科学基金项目(ZR2021ZD09)

111项目(B20048)

收起

High-precision seafloor topographic mapping based on data-knowledge-driven: An example from the South China Sea

  • LIU Yang , 1, 2 ,
  • LI Sanzhong , 1, 2, * ,
  • ZOU Zhuoyan 1, 2 ,
  • SUO Yanhui 1, 2 ,
  • SUN Yi 1, 2
Expand
  • 1. Frontiers Science Center for Deep Ocean Multispheres and Earth System, Key Lab of Submarine Geosciences and Prospecting Techniques, MOE and College of Marine Geosciences, Ocean University of China, Qingdao 266100, China
  • 2. Laboratory for Marine Mineral Resources, Laoshan Laboratory, Qingdao 266237, China

Received date: 2023-09-27

  Revised date: 2024-05-22

  Online published: 2024-11-25

Fold

摘要

海底地形具有非常重要的商业、工程、军事和科学研究价值。目前,常用重力场数据反演海底地形,如自由空气重力异常和垂直重力梯度。然而,由于现有方法反演海底地形具有较强的多解性,仍然无法准确获取高精度的海底地形。该文提出了重力-密度法与随机森林结合的数据-知识驱动新方法,以重建准确的海底地形。该方法在中国南海海域进行了测试,并与重力-密度法、随机森林以及现有的SIO模型进行了对比分析。反演结果显示,数据-知识驱动提供了更好的反演性能,随机森林和重力-密度法次之,SIO模型最差。相比于重力-密度法,数据-知识驱动的平均绝对误差、平均相对误差和均方根误差分别降低了21%、25%和7%;而相比于随机森林,它们分别也降低了20%、20%和20%。此外,数据-知识驱动模型与船载测深数据具有较高的一致性,其差值大约有72%分布在±10 m范围内,占比高于其他三种模型。该结果证明了数据-知识驱动方法在海底地形反演中的可行性和有效性,有助于加快高精度海底地形的绘制。

关键词： 海底地形; 机器学习; 数据驱动; 知识驱动; 重力-密度法; 随机森林; SIO模型; 船载测深

本文引用格式

刘洋 , 李三忠 , 邹卓延 , 索艳慧 , 孙毅 . 基于数据-知识驱动的高精度海底地形绘制:以南海为例[J]. 海洋学研究, 2024 , 42(3) : 142 -152 . DOI: 10.3969/j.issn.1001-909X.2024.03.012

Abstract

Seafloor topography is of considerable value in commercial, engineering, military and scientific research. Currently, gravity field data, such as free air gravity anomalies and vertical gravity gradients, are commonly used to inverse seafloor topography. However, due to the strong multi-resolution of the existing methods to inverse seafloor topography, it is still impossible to obtain accurate high-precision seafloor topography. A new data-knowledge-driven method was proposed to reconstruct accurate seafloor topography, which combines the gravity-density method with random forests. This method was applied to the South China Sea and compared with the gravity-density, random forest, and existing SIO models. The inversion results show that the data-knowledge-driven method provides better inversion performance, followed by the random forest and gravity-density methods, and the SIO model is the worst. The mean absolute error, mean relative error and root mean square error of the data-knowledge-driven are reduced by 21%, 25% and 7%, respectively, compared to those of the gravity-density method, while they are also reduced by 20%, 20% and 20%, respectively, compared to those of the random forest. In addition, the data-knowledge-driven model has a high degree of agreement with the shipboard bathymetry data, with approximately 72% of its differences distributed within ±10 m, which is higher than that of the other three models. The results demonstrate the feasibility and effectiveness of the data-knowledge-driven approach in seafloor topography inversion, which helps to accelerate the mapping of high-precision seafloor topography.

Key words： seafloor topography; machine learning; data-driven; knowledge-driven; gravity-density method; random forest; SIO model; shipboard bathymetry

0 引言

上百年的海底地形探测和研究历史表明,绘制精确的海底地形不仅在理解海洋地质、海洋地球物理、海洋环流、海洋灾害、海洋生物方面可发挥重要作用,还有助于航运安全、潜艇航行[1]。海底山脉对航行构成威胁,但也蕴藏着稀土矿物,为深海采矿者的商业目标;陡峭的海山还是海洋生物的重要绿洲,被誉为珊瑚和其他海洋生物生存生活的摩天大楼;海山的大小和成簇、成群、成链的分布也为板块运动和岩浆活动的研究提供了丰富的信息与成因线索。这些海山不仅为海底生命提供物质和能量,还构建了深层水和底层水的流动格局以及物质、能量输运路径,也组成了一个个相对孤立的海底生态系统,是深海海底流固耦合的重要形式,因而引起了各国的高度重视。例如,日本赞助的“海床2030”计划就是鼓励个人爱好者积极参与绘制高清海底地形图。
从技术层面看,20世纪50年代至今,海底地形多是通过船载的单波束和多波束回声探测仪测量的。尽管船载测深提供了高精度、高分辨率的海底地形,但是船载测深的效率低且成本高。迄今为止,船载测深的海洋区域仅占全球海域的20%[2],还有相当一部分的海底探测空白区。据估计,在全球海域使用船载测深可能需要花费上百年的时间,且会消耗巨大的人力和物力[3]。此外,机载激光雷达和遥感图像预测具有较高的测深效率,但是它们仅适用于浅海且易受到外部环境的影响[4-5]。幸运的是,卫星测高技术为构建高精度的海底地形提供了新手段,可以加快海底地形的绘制速度[6⇓-8]。
卫星测高技术可以在任何天气条件下不间断地提供真实、完整、全球性和精确的海面数据。从卫星测高数据中获得的重力场是预测海水深度的有效工具。随着卫星测高数据精度和密度的提高,使用重力场数据开发的全球海底模型越来越多,例如ETOPO1[9]、GBECO[10]、SIO(Scripps Institute of Oceanography,斯克里普斯海洋研究所)[11]、DTU(Denmarks Tekniske Universitet,丹麦科技大学)[12]、SRTM30_PLUS[13]和BAT_WHU2020[14]。目前,利用重力场数据反演海底地形的方法主要包括重力-密度法[15⇓-17]、导纳函数法[18]、Smith & Sandwell法[11]以及最小二乘配置法[7,19]。一系列的对比实验表明,在相同分辨率下,重力-密度法比其他方法更简单、更准确[20-21]。该方法是根据少数船载测深数据和自由空气重力异常数据反演海底地形,其关键在于海底洋壳与海水密度差异的确定,已应用于多个海域[22⇓-24]。另外,学者们也在努力改进现有方法以获取更高精度的海底地形[25⇓-27]。但是,重力场与海底地形之间的复杂函数关系很难进行准确的表征[28-29]。因此,仍然需要新方法来构建更精确的海底地形。
机器学习以强大的非线性映射能力在地球科学研究领域中表现出巨大的潜力[30-31]。与其他方法不同,机器学习以数据为驱动力,可以自主学习重力场数据与海底地形之间的非线性关系,而不需要额外的物理知识。机器学习已经成功地应用于海底地形重建,如ANNAN等[25]使用卷积神经网络和测高衍生的重力场数据,提高了几内亚湾的海底地形精度。SUN等[26]利用反向传播神经网络学习多源重力数据(自由空气重力异常和垂直重力梯度)与海水深度之间的映射关系,成功提高了马里亚纳海沟地区的地形精度。YANG等[32]将重力场数据和其他地球物理数据(磁异常和海底年龄)同时作为机器学习的输入,获得了几内亚湾的高精度地形。上述研究证明了机器学习的有效性,并进一步促进了用重力场数据重建海底地形的探索。尽管机器学习以数据驱动的方式提高了海底地形的反演精度,但是它仍然面临数据稀缺和场景复杂导致的准确性和稳定性低的问题[33]。事实上,简单地直接应用机器学习很难获得所需的反演性能。因此,嵌入物理知识为机器学习提供更丰富的信息是提高反演性能的一种实用方法[34⇓-36]。
本文尝试联合使用随机森林和重力-密度法,构建数据-知识驱动的反演方法,以建立海底地形与地球物理数据之间的映射关系。该方法使用地球物理数据作为输入特征,包括自由空气重力异常、垂直重力梯度、均衡重力异常和磁异常,对海底地形进行预测。此外,重力-密度法的反演结果被视为物理约束,并作为新特征和地球物理数据一起输入到随机森林以获得物理一致的结果。以南海作为研究区域,采用数据-知识共同驱动的智能方法构建了分辨率为1'×1'的测深模型。同时,对优化后的模型进行了比较,探讨了数据驱动、知识驱动和数据-知识驱动方法对海底地形重建的影响。

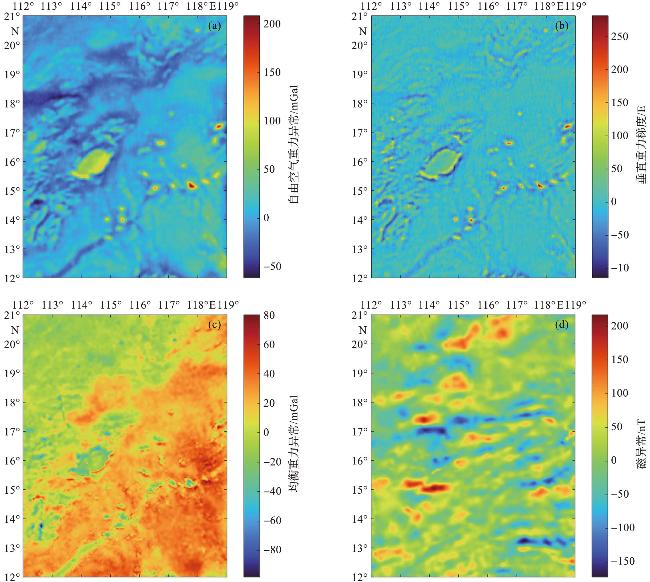
1 区域背景和数据汇编

中国南海是太平洋最西边的一个边缘海,位于欧亚板块、印度洋-澳大利亚板块和太平洋板块的交界处,其外形似呈NE—SW向延伸的半封闭海[37-38]。本文的研究区范围为112°E—119°E,12°N—21°N(图1)。该区域内海底构造复杂,地形起伏大,发育有海底高原、海山、海丘、海槽、海沟等构造地貌,还蕴含丰富的矿产资源,获取其高精度的海底地形意义重大。
图1 船载测深数据分布

(蓝色点和橙色点分别代表控制点和检查点,背景为SIOv25.1的水深模型。)

Fig.1 Distribution of shipboard bathymetric data

(The blue and orange points represent control and check points, respec-tively, with the bathymetric model of SIOv25.1 in the background.)

本文使用的数据包括船载测深数据、重力场数据和其他地球物理数据。船载测深数据包括单波束和多波束探测数据。它们均来自美国国家地球物理数据中心(National Geophysical Data Center,NGDC, https://www.ncei.noaa.gov/maps/trackline-geophysics),共包含74次巡航调查数据。为了保证船载测深数据的质量,需要对其进行预处理以删除异常值。使用公开的测深模型SIOv25.1(https://topex.ucsd.edu/pub/)作为数据质量控制的先验模型,删除绝对误差大于两倍均方根误差或相对误差大于0.5的船载测深数据。
经过预处理后,137 998个测深数据点被获取,其中27 599(20%)个数据点作为检查点(图1中橙色点),剩余的110 399(80%)个数据点作为构建测深模型的控制点(图1中蓝色点)。控制点和检查点相互不重复且在研究区域内均匀分布。重力场数据包括自由空气重力异常和垂直重力梯度,可从美国斯克里普斯海洋研究所的网站(https://topex.ucsd.edu/pub/)下载。本文使用了2023年发布的32.1版重力场数据。自由空气重力异常由卫星测高数据计算获得,其分辨率为1',精度为1~2 mGal;垂直重力梯度由重力异常估算而来,其分辨率为1'[39]。其他地球物理数据包括均衡重力异常[40]和磁异常[41],其分辨率均为1',从EarthByte Group网站下载获取(https://www.earthbyte.org/)。研究区地球物理数据的分布如图2所示,其统计分析结果如表1所示。由于这些地球物理数据对预测海底地形具有一定的潜在贡献,故将其作为随机森林的输入特征。
图2 研究区的地球物理数据分布

Fig.2 Distribution of geophysical data in the study area

表1 研究区地球物理数据的统计分析

Tab.1 Statistical analysis of geophysical data in the study area

特征参数 最大值 最小值 平均值 标准差
自由空气重力异常/mGal 207.90 -60.64 4.87 19.66
垂直重力梯度/E 281.23 -114.34 0.34 19.97
均衡重力异常/mGal 80.38 -97.52 14.13 18.56
磁异常/nT 217.55 -172.32 5.95 43.39

2 方法

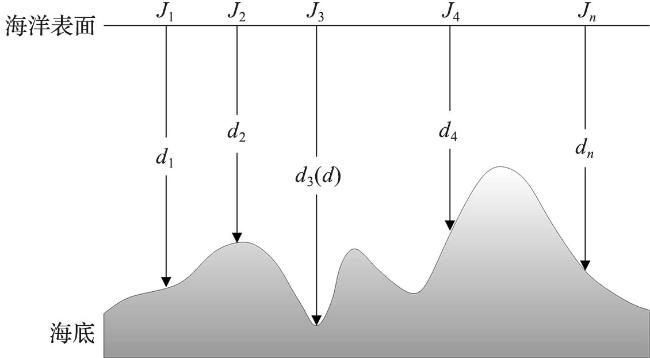
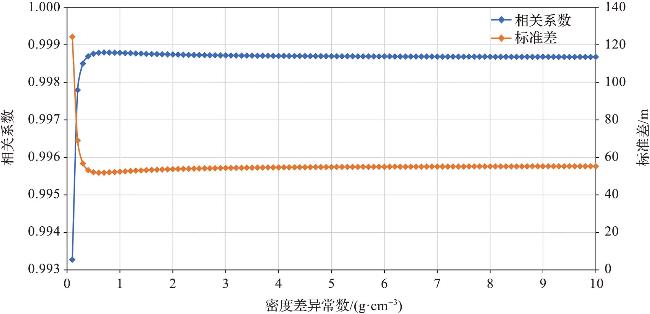
2.1 重力-密度法

海底地形和重力异常之间存在非线性映射关系[42]。非线性问题可以通过使用合适的“参考场”和“残差场”进行线性化来解决[43],其原理是将重力异常分解为长波分量和短波分量。长波分量是由地球深部物质的质量变化产生的参考重力场,短波分量是由地球表面局部基岩变化产生的残差重力场[15,44]。合并长波重力参考值和短波重力残差值可计算获得观测的重力异常,公式如下:
Δgobs=Δgshort+Δglong
式中:Δgobs为观测的重力异常,单位为mGal;Δgshort为短波重力异常,单位为mGal;Δglong为长波重力异常,单位为mGal。
重力-密度法的原理如图3所示,其中J1,J2,J3,…,Jn为海域内的船载测深点,对应的海水深度为d1,d2,d3,…,dn,d为参考深度,一般为船舶测深中的最大海水深度。根据布格板公式[45],船测点Jn的短波重力异常可用下式计算:
Δ g J n s h o r t=2πGΔρ(dn-d)
式中:Δ g s h o r t J n为对应船载测深处的短波重力异常;G为万有引力常数,通常取为6.672×10-8 cm3/g·s2;Δρ为海底洋壳和海水的密度差异常数。
图3 重力-密度法的原理示意图

Fig.3 Schematic diagram of the principle of gravity-density method

根据公式(1)和公式(2),船测点的长波重力异常可以通过观测的重力异常减去短波重力异常获得。然后,利用合适的插值方法获得研究区域内任意一点i处的长波重力异常,进而获得研究区域内任意一点i处的短波重力异常,公式如下:
Δ g i s h o r t=Δ g i o b s-Δ g i l o n g
di= Δ g i s h o r t 2 π G Δ ρ+d
重力-密度法在计算过程中只涉及密度差异常数和参考深度。一般而言,参考深度是一个参考量,其取值对反演精度影响较小;而密度差异常数对反演精度影响较大,是该方法的关键参数[46]。由于不同海域的海水密度和海底洋壳密度存在差异,所以需要针对研究区域估算密度差异常数。延拓法和迭代法是确定密度差异常数常用的两种方法。延拓法计算密度差异常数时存在多解性和不稳定性等问题,因此本文使用迭代法确定密度差异常数。迭代法是利用控制点计算出不同密度差异常数下的水深模型,然后利用插值方法计算检查点的海水深度并与船载测量结果进行比较,选取标准差最小、相关系数最大对应的密度差异常数作为该研究区域的最优值。图4显示了研究区标准差和相关系数随着密度差异常数变化的趋势。最终,本文选取的密度差异常数为0.7 g/cm3。
图4 不同密度差异常数下重力-密度法与船载测深之间的相关系数和标准差

Fig.4 Correlation coefficients and standard deviations between gravity-density method and shipboard bathymetry for different density difference constants

2.2 随机森林算法

随机森林是一种常见的机器学习方法,运用了集成学习的思想[47]。它旨在通过组合大量决策树来提升分类或回归精度。决策树是一种无参数有监督的机器学习算法,其模型呈现树状结构。集成学习思想是针对单个弱模型所提出,利用多个弱模型的优势构建一个强大的机器学习模型。随机森林是若干个决策树模型的平均结果。随机森林的具体构建步骤如下。
1)样本抽取。采用Bootstrap法从原始数据集中有放回地随机抽取N个训练子集,保证每个训练子集与原始数据集的数据容量一致,从而为每棵决策树生成训练数据。
2)决策树建立。对抽样获取的N个训练子集建立N棵决策树,每棵决策树任意生长,无需剪枝处理。在每棵树生长过程中,从M个特征中等概率随机抽取m个特征作为一个特征子集(通常m取log2M+1)。然后,从训练子集中选择最优特征对节点进行分割。
3)平均值求取。根据构建的N棵决策树对待测数据进行预测,汇总N棵决策树的预测结果并求取平均值,平均值将作为随机森林的最终输出结果。
随机森林在机器学习算法中具有较强的抗过拟合和抗干扰能力,即使面对噪声较大的数据集也能有较好的预测效果。本文使用Python中的scikit-learn实现基于两种驱动方式的随机森林模型,即数据驱动和数据-知识驱动。将物理知识嵌入机器学习中有多种方式,其中把物理知识预测的结果作为新特征输入机器学习模型是一种常用手段。本文是把重力-密度法和随机森林相结合以更好地约束模型。
基于数据驱动的随机森林的输入数据为经度、纬度、自由空气重力异常、垂直重力梯度、均衡重力异常和磁异常;而基于数据-知识驱动的随机森林的输入数据需要额外融入重力-密度法的反演结果。同时,采用最大最小归一化使输入数据缩小范围至0~1。此外,随机森林需要调整5个参数,包括n_eatimators、max_depth、max_features、min_samples_leaf、min_samples_split,各参数的含义可见文献[47]。为了找到5个参数的最佳值,利用网格搜索法和交叉验证技术对它们进行了优化。经过网格搜索后,基于两种驱动方式的随机森林模型的最优参数如表2所示。
表2 基于两种驱动方式的随机森林的最优参数

Tab.2 Optimal parameters for random forests based on two driving methods

参数 最优值
数据驱动 数据-知识驱动
n_eatimators 1 000 1 000
max_depth 60 50
max_features 4 3
min_samples_leaf 1 2
min_samples_split 2 2

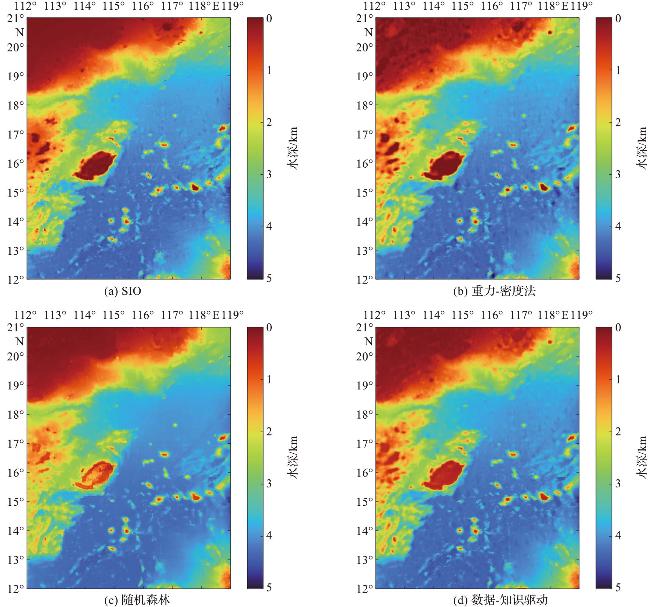
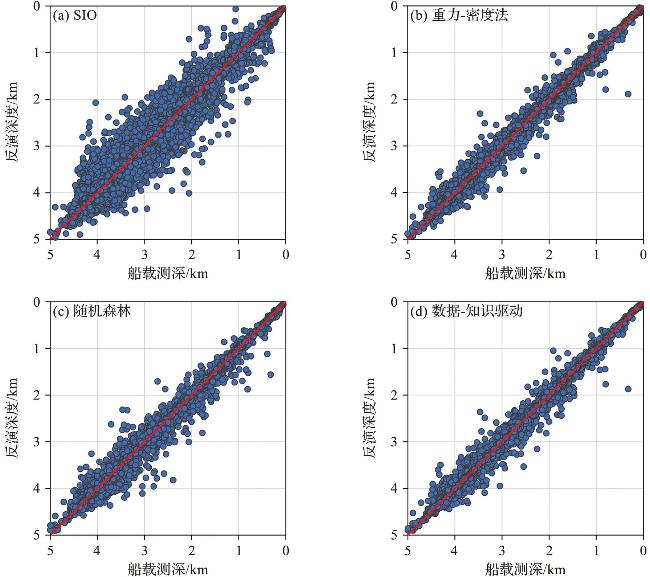
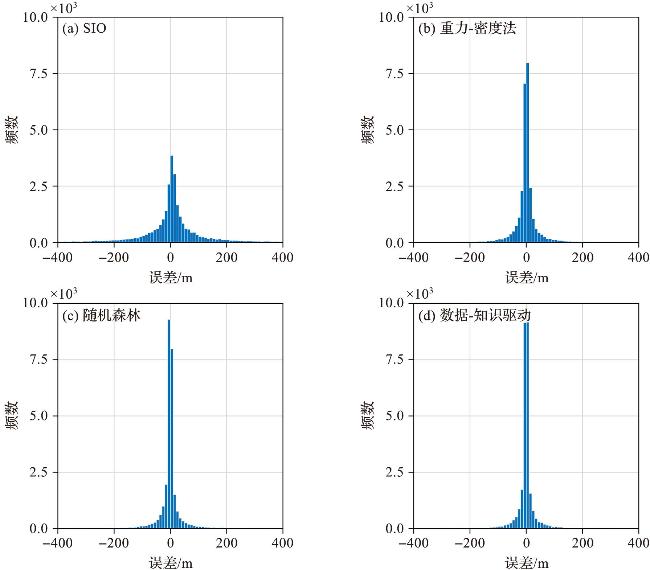
3 结果分析

本文提出了随机森林和重力-密度法结合的数据-知识驱动模型,并与数据驱动的随机森林(后文简称随机森林)、重力-密度法以及现有的SIO模型进行了比较。图5显示了各种模型重建的分辨率为1'×1'的南海海底地形。重建结果显示四种模型重建的海底地形较为接近,都能够清晰地描绘出南海海域的大陆架、海山、海沟和海盆等地形地貌,其中数据-知识驱动模型最为精细,随机森林和重力-密度法次之,SIO模型最差。在中沙群岛(113.8°E—115°E,15.5°N—16.5°N)附近区域,四种模型重建的海底地形存在明显差异。在该区域附近,重力-密度法模型受到船载测深点数量以及密度差异常数的限制,重建的海底地形可能存在偏差(图5b)。随机森林重建的海底地形显示中沙群岛向下凹陷(图5c),不符合实际的地形分布规律,说明数据驱动模型的物理一致性较差,同样是由于该区域数据稀缺导致了准确性降低。而数据-知识驱动模型既能保持重建海底地形的准确性又能符合实际的地形分布规律(图5d)。
图5 四种模型反演的研究区海底地形

Fig.5 Seafloor topography of the study area by four models

本文使用了平均绝对误差、平均相对误差、均方根误差以及相关系数四个指标来评估四种模型反演的海底地形的准确性,其中前三个指标越小表示反演精度越高,最后一个指标越接近1表示反演效果越好。由评估结果(表3)可知,相比于重力-密度法、随机森林以及数据-知识驱动模型,SIO模型的评估结果较差,其平均绝对误差、平均相对误差和均方根误差是其他方法的3倍左右。尽管重力-密度法获取了相对较好的评估结果,但是随机森林的平均绝对误差和平均相对误差比其更低,说明了机器学习方法也可以准确反演海底地形,无需通过迭代法确定密度差异常数。然而,随机森林的均方根误差和相关系数结果略差于重力-密度法,说明随机森林反演的海底地形存在异常值,偏离了船载测深值。数据-知识驱动模型的评估结果最优,其平均绝对误差为19.65 m,平均相对误差为0.82%,均方根误差为53.34 m,相关系数为0.999 0。相比于重力-密度法,数据-知识驱动模型的平均绝对误差、平均相对误差和均方根误差分别降低了21%、25%和7%;而相比于随机森林,它们分别降低了20%、20%和20%。这表明数据-知识驱动模型能够有效提高海底地形的反演精度。
表3 四种模型的评估指标

Tab.3 Evaluation indexes for the four models

评估指标 SIO 重力-密度法 随机森林 数据-知识驱动
平均绝对误差/m 83.18±138.66 24.86±51.85 24.51±62.02 19.65±49.59
平均相对误差/% 3.47±7.17 1.09±4.07 1.03±4.09 0.82±3.81
均方根误差/m 161.69 57.50 66.68 53.34
相关系数 0.990 5 0.998 8 0.998 4 0.999 0
进一步分析深度反演值与真实值之间的差距可知,SIO模型反演的深度与船载测深之间的一致性较差,而数据-知识驱动模型显示出较好的一致性(图6)。从整体观察,SIO模型反演结果与船载测深之间存在较大误差,数据点比较分散(图6a);而其他三种模型的数据点集中分布在对角线附近(图6b~6d)。仔细观察可以看出重力-密度法和随机森林的反演结果也存在一些明显的异常值(图6b、6c)。相比于重力-密度法,随机森林模型可自动学习海底地形与地球物理数据之间的映射关系,无需确定密度差异常数。另外,它们结合形成的数据-知识驱动模型更有效地提高了海底地形反演精度,反演结果与船载测深更加吻合(图6d),这既解决了数据驱动缺乏物理意义的问题,又解决了知识驱动精度低的问题。
图6 船载测深与模型反演深度的比较

Fig.6 Comparison of shipboard bathymetry and inversion depths by four models

统计船载测深和模型反演结果的差值分布更有助于评估各种模型的优劣。图7展示了船载测深和反演结果的差值统计直方图。从图中可以看出,各种模型反演的地形与船载测深结果的差值均呈现钟形分布,可以认为差值近似服从正态分布。重力-密度法、随机森林和数据-知识驱动都显示出相似的正态分布形态,优于SIO模型的正态分布。经过统计分析,SIO模型、重力-密度法、随机森林和数据-知识驱动的反演地形与船载测深结果的绝对误差在10 m以内的占比分别约为34%,63%,68%和72%,表明了数据-知识驱动中有更多的差值接近于0,说明数据-知识驱动反演的海底地形更接近实际测量值。
图7 四种模型的反演结果与船载测深的差值统计直方图

Fig.7 Histogram of the difference statistics among the inversion results of the four models and shipboard bathymetry

4 结论

本文联合使用随机森林和重力-密度法构建了数据-知识驱动反演模型,智能学习海底地形与地球物理数据之间的非线性关系,并以南海局部海域(112°E—119°E,12°N—21°N)作为研究区域,与SIO模型、随机森林和重力-密度法进行了对比分析,得到以下结论。
1)随机森林和重力-密度法的反演结果均能清晰描绘南海的复杂地形,优于SIO模型。从评估指标看,随机森林的平均绝对误差和平均相对误差优于重力-密度法,而均方根误差和相关系数劣于重力-密度法。此外,随机森林可自主地学习海底地形与地球物理数据之间的非线性映射关系,无需额外的物理知识;而重力-密度法需要使用迭代法确定密度差异常数,具有明确的物理意义。
2)数据-知识驱动结合了随机森林和重力-密度法的优势,有效提高了海底地形反演精度。从整体上看,数据-知识驱动的反演精度优于SIO模型、随机森林和重力-密度法,可以更加准确地反演海底地形。相比于重力-密度法,数据-知识驱动的四个评估指标均有提升,并且绝对误差小于10 m的占比约为72%,高于其它模型。
3)嵌入物理知识的机器学习应用于海底地形反演有助于提高模型的可靠性和可解释性,可以更好地理解海底地形与地球物理数据之间的关系。本文仅仅将重力-密度法的反演结果作为新特征输入随机森林,并应用于南海局部海域。在未来,应充分考虑物理知识融入机器学习的方式以及它们应用于海底地形反演的泛化能力,这将有助于推动高精度海底地形的绘制。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
WÖLFL A C, SNAITH H, AMIREBRAHIMI S, et al. Seafloor mapping-the challenge of a truly global ocean bathymetry[J]. Frontiers in Marine Science, 2019, 6: 283.

[2]
SANDWELL D T, SMITH W H, GILLE S, et al. Bathymetry from space: White paper in support of a high-resolution, ocean altimeter mission[J]. International Geophysics Series, 2001, 69: 1049-1062.

[3]
SMITH W. Introduction to this special issue on bathymetry from space[J]. Oceanography, 2004, 17(1): 6-7.

[4]
PEERI S, GARDNER J V, WARD L G, et al. The seafloor: A key factor in lidar bottom detection[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(3): 1150-1157.

[5]
EUGENIO F, MARCELLO J, MARTIN J. High-resolution maps of bathymetry and benthic habitats in shallow-water environments using multispectral remote sensing imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(7): 3539-3549.

[6]
黄谟涛, 翟国君, 欧阳永忠, 等. 卫星测高技术应用研究回顾与展望[J]. 海洋测绘, 2004, 24(4):65-70.

HUANG M T, ZHAI G J, OU-YANG Y Z, et al. Review and prospect of application study in altimetry[J]. Hydrographic Surveying and Charting, 2004, 24(4): 65-70.

[7]
CALMANT S, BERGE-NGUYEN M, CAZENAVE A. Global seafloor topography from a least-squares inversion of altimetry-based high-resolution mean sea surface and shipboard soundings[J]. Geophysical Journal International, 2002, 151(3): 795-808.

[8]
TOZER B, SANDWELL D T, SMITH W H F, et al. Global bathymetry and topography at 15Arc Sec: SRTM15+[J]. Earth and Space Science, 2019, 6(10): 1847-1864.

[9]
AMANTE C, EAKINS B W. ETOPO1 arc-minute global relief model: Procedures, data sources and analysis[R]//NOAA Technical Memorandum NESDIS NGDC-24. NOAA, National Geophysical Data Center, 2009.

[10]
MARKS K M, SMITH W H F, SANDWELL D T. Evolution of errors in the altimetric bathymetry model used by Google Earth and GEBCO[J]. Marine Geophysical Researches, 2010, 31(3): 223-238.

[11]
SMITH W H F, SANDWELL D T. Global sea floor topography from satellite altimetry and ship depth soundings[J]. Science, 1997, 277(5334): 1956-1962.

[12]
ANDERSEN O B, KNUDSEN P. The DNSC08BAT bathy-metry developed from satellite altimetry[C]// Proceedings of the EGU-2008 Meeting: Vienna, Austria, 2008.

[13]
BECKER J J, SANDWELL D T, SMITH W H F, et al. Global bathymetry and elevation data at 30 arc seconds resolution: SRTM30_PLUS[J]. Marine Geodesy, 2009, 32(4): 355-371.

[14]
胡敏章, 张胜军, 金涛勇, 等. 新一代全球海底地形模型BAT_WHU2020[J]. 测绘学报, 2020, 49(8):939-954.

DOI

HU M Z, ZHANG S J, JIN T Y, et al. A new generation of global bathymetry model BAT_WHU2020[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(8): 939-954.

DOI

[15]
HSIAO Y S, KIM J W, KIM K B, et al. Bathymetry estimation using the gravity-geologic method: An investi-gation of density contrast predicted by the downward continuation method[J]. Terrestrial, Atmospheric and Oceanic Sciences, 2011, 22(3): 347.

[16]
KIM J W, VON FRESE R R B, LEE B Y, et al. Altimetry-derived gravity predictions of bathymetry by the gravity-geologic method[J]. Pure and Applied Geophysics, 2011, 168(5): 815-826.

[17]
欧阳明达. 利用海洋重力数据反演海底地形的理论与方法[D]. 郑州: 解放军信息工程大学, 2015.

OU-YANG M D. Theory and method of inversion of seabed topography using marine gravity data[D]. Zhengzhou: PLA Information Engineering University, 2015.

[18]
MCNUTT M. Compensation of oceanic topography: An application of the response function technique to the surveyor area[J]. Journal of Geophysical Research: Solid Earth, 1979, 84(B13): 7589-7598.

[19]
ARABELOS D, TZIAVOS I N. Gravity-field improvement in the Mediterranean Sea by estimating the bottom topography using collocation[J]. Journal of Geodesy, 1998, 72(3): 136-143.

[20]
KIM K B, HSIAO Y S, KIM J W, et al. Bathymetry enhancement by altimetry-derived gravity anomalies in the East Sea (Sea of Japan)[J]. Marine Geophysical Researches, 2010, 31(4): 285-298.

[21]
李倩倩, 鲍李峰. 测高重力场反演海底地形方法比较[J]. 海洋测绘, 2016, 36(5):1-4,18.

LI Q Q, BAO L F. Comparative analysis of methods for bathymetry prediction from altimeter-derived gravity anomalies[J]. Hydrographic Surveying and Charting, 2016, 36(5): 1-4, 18.

[22]
胡敏章, 李建成, 金涛勇. 应用重力地质方法反演皇帝海山的海底地形[J]. 武汉大学学报:信息科学版, 2012, 37(5):610-612,629.

HU M Z, LI J C, JIN T Y. Bathymetry inversion with gravity-geologic method in Emperor Seamount[J]. Geomatics and Information Science of Wuhan University, 2012, 37(5): 610-612, 629.

[23]
王永康, 周兴华, 唐秋华, 等. 应用重力地质法反演马里亚纳海沟地形[J]. 海洋科学进展, 2020, 38(4):708-716.

WANG Y K, ZHOU X H, TANG Q H, et al. Predicting bathymetry in Mariana trench using gravity-geologic method[J]. Advances in Marine Science, 2020, 38(4): 708-716.

[24]
欧阳明达, 孙中苗, 翟振和. 基于重力地质法的南中国海海底地形反演[J]. 地球物理学报, 2014, 57(9):2756-2765.

DOI

OU-YANG M D, SUN Z M, ZHAI Z H. Predicting bathymetry in South China Sea using the gravity-geologic method[J]. Chinese Journal of Geophysics, 2014, 57(9): 2756-2765.

[25]
ANNAN R F, WAN X Y. Recovering bathymetry of the gulf of Guinea using altimetry-derived gravity field products combined via convolutional neural network[J]. Surveys in Geophysics, 2022, 43(5): 1541-1561.

[26]
SUN Y J, ZHENG W, LI Z W, et al. Improved the accuracy of seafloor topography from altimetry-derived gravity by the topography constraint factor weight optimization method[J]. Remote Sensing, 2021, 13(12): 2277.

[27]
AN D C, GUO J Y, LI Z, et al. Improved gravity-geologic method reliably removing the long-wavelength gravity effect of regional seafloor topography: A case of bathymetric prediction in the South China Sea[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 4211912.

[28]
CALMANT S, BAUDRY N. Modelling bathymetry by inverting satellite altimetry data: A review[J]. Marine Geophysical Researches, 1996, 18(2): 123-134.

[29]
WANG Y M. Predicting bathymetry from the earth’s gravity gradient anomalies[J]. Marine Geodesy, 2000, 23(4): 251-258.

[30]
REICHSTEIN M, CAMPS-VALLS G, STEVENS B, et al. Deep learning and process understanding for data-driven earth system science[J]. Nature, 2019, 566(7743): 195-204.

[31]
SHEN C P, APPLING A, GENTINE P, et al. Differentiable modelling to unify machine learning and physical models for geosciences[J]. Nature Reviews Earth & Environment, 2023, 4: 552-567.

[32]
YANG L, LIU M, LIU N, et al. Recovering bathymetry from satellite altimetry-derived gravity by fully connected deep neural network[J]. IEEE Geoscience and Remote Sensing Letters, 2023, 20: 1502805.

[33]
CHEN Y, ZHANG D. Integration of knowledge and data in machine learning[Z/OL]. arXiv, 2022: 2202. 10337. https://arxiv.org/abs/2202.10337.

[34]
KARPATNE A, ATLURI G, FAGHMOUS J H, et al. Theory-guided data science: A new paradigm for scientific discovery from data[J]. IEEE Transactions on Knowledge and Data Engineering, 2017, 29(10): 2318-2331.

[35]
GETTELMAN A, GEER A J, FORBES R M, et al. The future of earth system prediction: Advances in model-data fusion[J]. Science Advances, 2022, 8(14): eabn3488.

[36]
MENG C Z, SEO S, CAO D F, et al. When physics meets machine learning: A survey of physics-informed machine learning[Z/OL]. arXiv, 2022: 2203. 16797. https://arxiv.org/abs/2203.16797v1.

[37]
MORTON B, BLACKMORE G. South China Sea[J]. Marine Pollution Bulletin, 2001, 42(12): 1236-1263.

PMID

[38]
WANG A M, DU Y, PENG S Q, et al. Deep water characteristics and circulation in the South China Sea[J]. Deep Sea Research Part I: Oceanographic Research Papers, 2018, 134: 55-63.

[39]
SANDWELL D T, MÜLLER R D, SMITH W H F, et al. Marine geophysics. New global marine gravity model from CryoSat-2 and Jason-1 reveals buried tectonic structure[J]. Science, 2014, 346(6205): 65-67.

DOI PMID

[40]
BALMINO G, VALES N, BONVALOT S, et al. Spherical harmonic modelling to ultra-high degree of Bouguer and isostatic anomalies[J]. Journal of Geodesy, 2012, 86(7): 499-520.

[41]
MAUS S, BARCKHAUSEN U, BERKENBOSCH H, et al. EMAG2: A 2-arc min resolution earth magnetic anomaly grid compiled from satellite, airborne, and marine magnetic measurements[J]. Geochemistry, Geophysics, Geosystems, 2009, 10(8). https://doi.org/10.1029/2009GC002471.

[42]
PARKER R L. The rapid calculation of potential anomalies[J]. Geophysical Journal International, 1973, 31(4): 447-455.

[43]
HWANG C. A bathymetric model for the South China sea from satellite altimetry and depth data[J]. Marine Geodesy, 1999, 22(1): 37-51.

[44]
KIM K B, YUN H S. Satellite-derived bathymetry prediction in shallow waters using the gravity-geologic method: A case study in the west sea of Korea[J]. KSCE Journal of Civil Engineering, 2018, 22(7): 2560-2568.

[45]
HSIAO Y S, HWANG C, CHENG Y S, et al. High-resolution depth and coastline over major atolls of South China Sea from satellite altimetry and imagery[J]. Remote Sensing of Environment, 2016, 176: 69-83.

[46]
STRYKOWSKI G, BOSCHETTI F, PAPP G. Estimation of the mass density contrasts and the 3D geometrical shape of the source bodies in the Yilgarn area, Eastern Goldfields, Western Australia[J]. Journal of Geodynamics, 2005, 39: 444-460.

[47]
BREIMAN L. Random forests[J]. Machine Learning, 2001, 45: 5-32.

Options
文章导航

/

〈 〉