0 引言
1 波高过阈样本选取
1.1 SSL法介绍
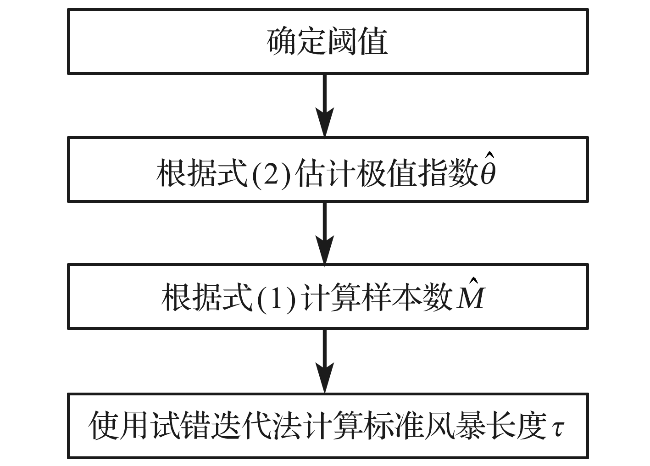
1.2 自动的标准风暴长度估计方法
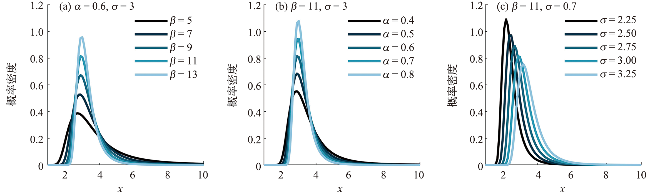
2 Gumbel-Pareto分布模型
3 工程算例
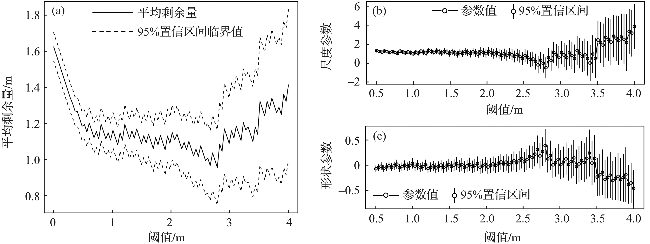
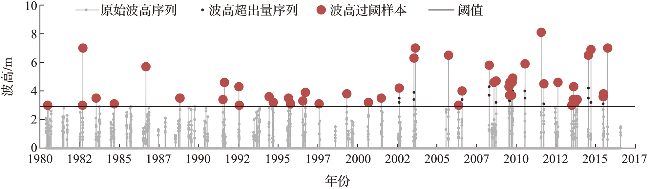
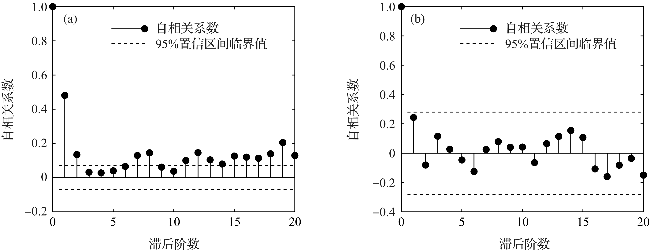
3.1 样本选取
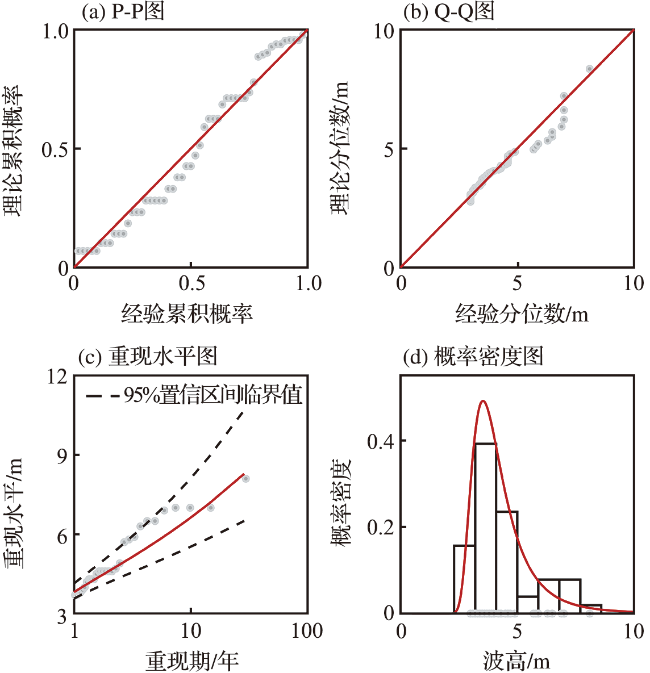
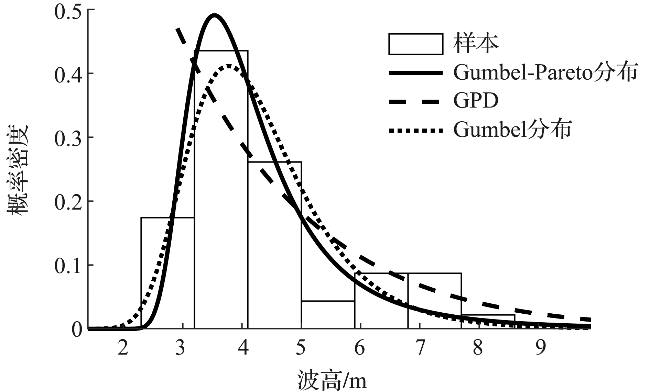
3.2 分布拟合与检验
表1 样本的主要统计特征量Tab.1 Main statistical characteristics of samples |
| 样本 | 尾部指数 | 均值/m | 方差/m2 | 偏度/m3 | 峰度/m3 |
|---|---|---|---|---|---|
| 波高过阈样本 | 3.059 | 4.351 | 1.798 | 1.092 | 3.124 |
| 波高年极值样本 | 9.958 | 4.610 | 2.611 | 0.437 | 2.354 |
表2 分布参数估计及K-S检验结果Tab.2 Results of parameters’ estimation and K-S tests |
| 样本 | 分布模型 | 参数 | 参数估计值 | K-S检验的p值 |
|---|---|---|---|---|
| 波高过阈 样本 | Gumbel-Pareto 分布 | β | 2.839 | 0.807 |
| α | 1.695 | |||
| σ | 3.677 | |||
| Gumbel 分布 | 尺度 | 0.894 | 0.419 | |
| 位置 | 3.772 | |||
| GPD | 形状 | 0.076 | 0.322 | |
| 尺度 | 2.120 | |||
| 位置 | 2.900 | |||
| 波高年极值 样本 | Gumbel-Pareto 分布 | β | 2.497 | 0.305 |
| α | 0.970 | |||
| σ | 3.584 | |||
| Gumbel 分布 | 尺度 | 1.362 | 0.689 | |
| 位置 | 3.855 | |||
| GPD | 形状 | 0.268 | 0.272 | |
| 尺度 | 3.110 | |||
| 位置 | 1.500 |
3.3 设计波高推算
表3 不同分布模型计算的20年、50年、100年和500年一遇设计波高Tab.3 20-, 50-,100-, 500-year return levels of design wave height calculated by different distribution models |
| 重现期/年 | 设计波高/m | ||
|---|---|---|---|
| Gumbel-Pareto分布 | Gumbel分布 | GPD | |
| 20 | 6.037 | 5.904 | 7.646 |
| 50 | 7.346 | 6.748 | 10.060 |
| 100 | 8.500 | 7.376 | 11.990 |
| 500 | 11.890 | 8.821 | 16.910 |