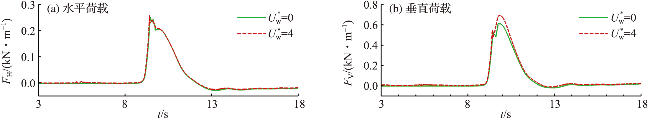Journal of Marine Sciences >

2023 , Vol. 41 >Issue 4: 32 - 45

DOI: https://doi.org/10.3969-j.issn.1001-909X.2023.04.004

Numerical simulation study on influences of onshore wind on overtopping characteristics of solitary wave under coastal seawall

  • ZHANG Liangbin , 1 ,
  • QU Ke , 1, 2, 3, * ,
  • HUANG Jingxuan 1 ,
  • WANG Xu 1 ,
  • GUO Lei 1
Expand
  • 1. School of Hydraulic and Environmental Engineering, Changsha University of Science & Technology, Changsha410114, China
  • 2. Key Laboratory of Dongting Lake Aquatic Eco-Environmental Control and Restoration of Hunan;Province, Changsha 410114, China
  • 3. Key Laboratory of Water-Sediment Sciences and Water Disaster Preventionof Hunan Province, Changsha 410114, China

Received date: 2023-02-10

  Revised date: 2023-10-23

  Online published: 2024-01-30

Fold

Abstract

Seawalls play an important role in protecting coastal towns from extreme waves damage. Based on two-dimensional incompressible two-phase flow numerical model, the influences of onshore wind on overtopping characteristics of solitary wave under coastal seawall were systematically studied in this paper. The reliability of the numerical model was verified by comparing the numerical results with experimental data, and the influencing factors such as onshore wind speed, incident wave height, crest freeboards of the coastal seawall, beach slope and seawall slope on the hydrodynamic process of solitary wave overtopping of coastal seawalls were discussed in detail. The research results show that with the increase of onshore wind speed, incident wave height and the decrease of crest freeboards of the coastal seawall, the maximum overtopping volume, maximum runup height and spatial distributions of the maximum water elevation gradually increase. With the increase of beach slope and seawall slope, the maximum overtopping volume increase and decrease, respectively, while the maximum runup height gradually increase. Onshore wind can affect the hydrodynamic characteristics of solitary wave overtopping of coastal seawall, increase the wave steepness and the wave crest propagation speed and cause the wave breaking earlier. Compared with the windless condition, the maximum wave overtopping volume, maximum runup height, maximum hydrodynamic forces and spatial distributions of the maximum water elevation are increased under onshore wind. The results of this study can provide a reference for the design of coastal engineering.

Key words： solitary wave; onshore wind; overtopping volume; numerical simulation; hydrodynamic characteristics

Cite this article

ZHANG Liangbin , QU Ke , HUANG Jingxuan , WANG Xu , GUO Lei . Numerical simulation study on influences of onshore wind on overtopping characteristics of solitary wave under coastal seawall[J]. Journal of Marine Sciences, 2023 , 41(4) : 32 -45 . DOI: 10.3969-j.issn.1001-909X.2023.04.004

0 引言

海啸通常由海底地震、火山爆发、海底滑坡或极端气候变化等引起[1⇓-3]。当海啸从远海传播至近岸时,受海底地形变化、水深变浅以及海岸建筑物等的影响,波浪产生变形,波高迅速增大,在海堤附近会发生越浪现象。当越浪量超过一定极值时,会对沿海城镇的基础设施和人民的生命安全造成严重威胁,如2004年的印度尼西亚海啸和2011年的东日本海啸产生的影响[4⇓⇓-7]。有学者认为孤立波与海啸有着相似的波形和水动力特性[8-9],因此近些年常用于模拟研究海啸等类似浅水大波与海岸工程建筑物之间的相互作用。
设计海堤时,一般采用物理模型实验或基于物理模型实验的经验公式来计算越浪量。1992年DE WAAL 等[10]对斜坡式海堤的越浪开展了物理模型实验的研究,提出了单斜坡的平均越浪量及最大越浪量的计算公式,并对岸滩坡度、水深以及堤顶超高等影响波浪爬高和越浪的因素进行了系统分析。HUNT[11]通过物理模型实验系统研究了波群、聚焦波以及孤立波作用下海堤的越浪特性,分析了入射波高与单宽越浪量之间的关系。随着计算机技术的发展,数值模拟计算方法被逐渐运用到波浪与海岸建筑物的相互作用中。HSIAO 等[12]和LIN 等[13]根据孤立波在海堤上越浪过程的三种基本形态,开展了一系列物理模型实验和数值计算,对孤立波的传播演变过程、海堤受力状况、越浪量以及最大爬高进行了系统性的测量与分析。张金牛 等[14]通过数值波浪水槽系统研究了孤立波在斜坡式海堤上越浪的水动力特性,分析了相对波高、相对超高等对越浪量的影响。曾婧扬 等[15]采用两相流模型对斜坡式海堤的越浪特性进行了研究,分析了堤顶超高和相对波高对越浪量的影响,给出了越浪流厚度和最大流速的分布形式和经验公式。王键 等[16]通过模拟不同断面尺寸带胸墙的斜坡堤越浪,分析了不同斜坡堤相关因素对平均越浪量的影响。万德成 等[17-18]采用流体体积函数法 (volume of fluid, VOF)对孤立波越过潜堤和直立柱的黏性流动进行了数值模拟。学者还通过数值模拟分析了向岸风对孤立波在不同建筑物上传播演变的影响,如海岸桥梁、不透水人工岛礁等,研究结果发现,向岸风对孤立波的传播变形、破碎有显著影响,会增大波浪冲击建筑物的水动力荷载[19⇓-21]。总体而言,目前对向岸风作用下孤立波在海堤上的越浪水动力过程的研究比较少。本文基于二维不可压缩两相流数值模型,系统研究了向岸风风速、入射波高、堤顶超高、岸滩坡度以及海堤坡度等因素对孤立波在斜坡式海堤上越浪水动力特性的影响,以期对海岸工程的防护提供参考。

1 控制方程和数值方法

1.1 控制方程

基于两相流数值模型,液体和空气均被认为是不可压缩的,流体的黏滞系数假定为常数,向岸风作用下孤立波与海堤之间的相互作用可用连续性方程和动量方程[22]进行表示:
∂ u i ∂ x i=0
∂ ρ u i ∂ t+ρuj ∂ u i ∂ x i=- ∂ p ∂ x i+ ∂ x j[μeff( ∂ u i ∂ x j+ ∂ u j ∂ x i)]+(ρ-ρref)gi
式中:ui和uj表示笛卡尔坐标系下的速度分量(i、j=1、2,分别表示二维流体运动的水平和垂直两个方向);xi和xj表示笛卡尔坐标系下的坐标分量;t表示时间;p表示静压;ρ表示混合流体密度,ρref表示参考密度;μl表示层流动力黏度,μt表示湍流动力黏度,有效动力黏度μeff=μl+μt;gi表示垂直方向上的重力加速度,取9.81 m·s-1。

1.2 数值方法

采用非结构化网格单元上的有限体积法对公式(1)和(2)进行离散。采用压力隐式算法(pressure implicit with splitting of operators, PISO)对压力和速度进行耦合求解[23]。采用一阶迎风格式和二阶伽马格式的加权组合方法对对流项进行离散[24-25]。为保证计算的精度和稳定性,采用动量平衡插值法[26]对控制单元从中心到表面进行速度插值,并利用二阶中心差分法对压力梯度项和扩散项进行离散。
采用WILOCX[27]的经典两方程中的k-ω湍流模型确定湍流动力黏度μt,并通过求解以下湍流运输方程得到湍动能k和湍流耗散率ω:
∂ ( ρ k ) ∂ t+ρuj ∂ k ∂ x j= ∂ ∂ x j[(μl+ μ t σ k) ∂ k ∂ x j]+2μt|S|2-ρkω
∂ ( ρ ω ) ∂ t+ρuj ∂ ω ∂ x j= ∂ ∂ x j[(μl+ μ t σ ω) ∂ ω ∂ x j]+2cμcω1ρ|S|2-cω2ρω2
式中:cμ、cω1、cω2、σω和σk为常数,cμ=0.09, c ω 1=5/9, c ω 2=5/6,σω=σk=2;S表示流体的应变率张量,|S|表示其数值的大小:
S= 1 2( ∂ u j ∂ x i+ ∂ u i ∂ x j)
采用VOF方法捕捉水和空气的交界面,控制方程如下:
∂ γ ∂ t+ ∂ ( γ u i ) ∂ x i=0
式中:γ表示网格单元中的水相体积分数,不同的水相体积分数值代表不同的含义。γ=1表示流体单元,γ=0表示空气单元,0<γ<1表示水和空气的混合单元。
计算域中,控制单元内的混合流体密度和层流动力黏度可用以下公式进行计算:
ρ=ρair+γ·(ρwater-ρair)
μl=μair+γ·(μwater-μair)
式中:ρair和ρwater分别表示空气和水的密度,μair和μwater分别表示空气和水的动力黏度。

2 数值模型验证

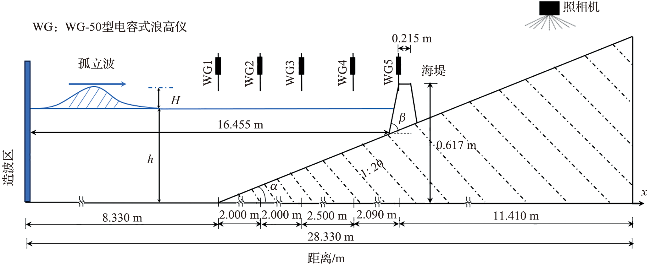
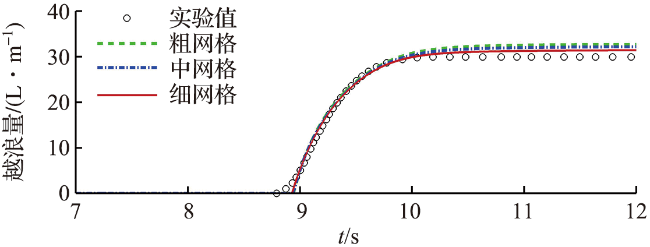
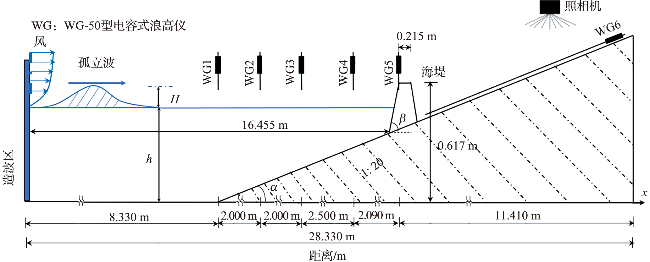
2.1 孤立波在斜坡式海堤上的越浪量验证

为验证数值模型计算孤立波在斜坡式海堤上越浪水动力过程的准确性,将数值计算结果与HUNT[11]的实验数据进行对比。实验区域布置如图1所示。模型水槽长36.000 m,宽27.000 m,高3.000 m,斜坡布置在距离造波区8.330 m处,海堤布置在距离斜坡坡脚8.125 m处,海堤两侧的坡度为1∶2,海堤的堤顶宽度为0.215 m,海堤的堤顶高度为0.617 m。实验中入射波高H为0.10 m,静止水深h为0.50 m,实验采用5个浪高仪(WG1~WG5)来测量孤立波在斜坡式海堤上的传播变形过程。进行数值模拟计算时,为验证网格无关性,采用三套不同分辨率的网格进行计算。数值模拟的孤立波波高时程曲线与实验数据的对比如图2所示,个别测点与实验数据有些许差异,可能是数值模型网格划分带来的离散误差所致,但总体上孤立波的波峰和波形与实验结果吻合较好。图3表示不同时刻的沿程水位高程的空间分布,通过对比发现,数值模拟的水位高程的沿程空间分布与实验结果吻合较好。孤立波的时程越浪量变化如图4所示,数值模型很好地模拟了孤立波在海堤上的越浪水动力过程。
图1 实验区域布置图[11]

Fig.1 Experimental layout[11]

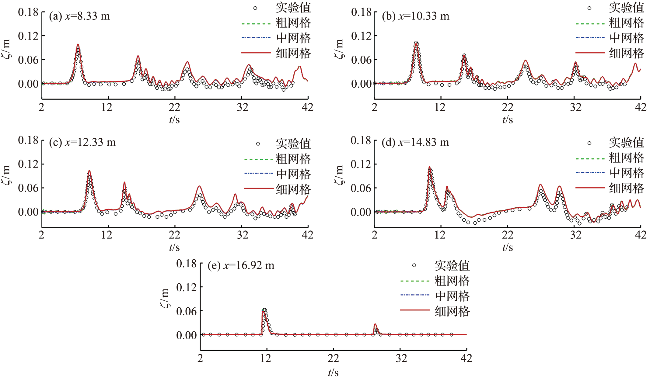
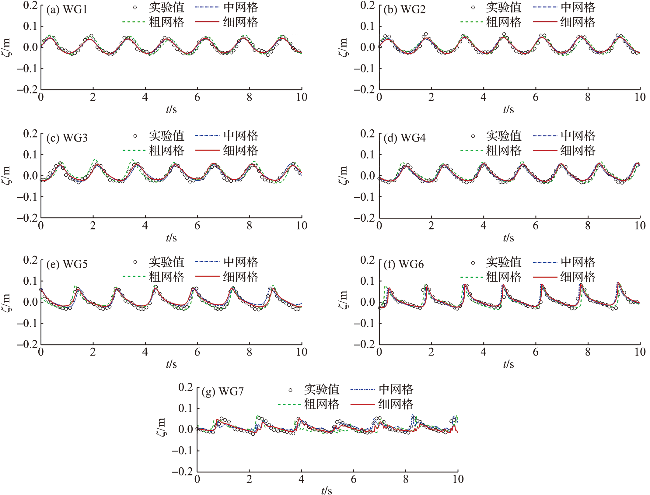
图2 不同测点处的波高时程曲线

Fig.2 The temporal evolution of wave height for different wave gauges

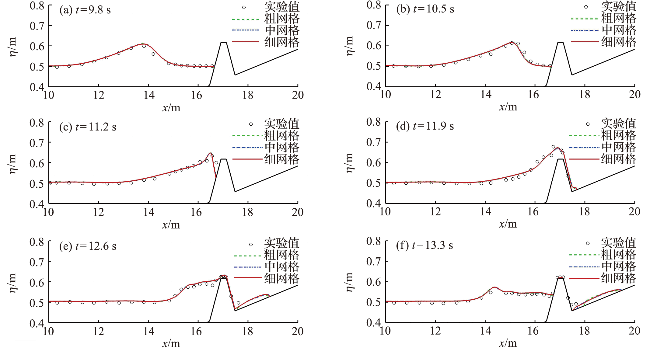
图3 不同时刻的沿程水位高程空间分布

Fig.3 Spatial distributions of wave elevation at different times

图4 孤立波的时程越浪量

Fig.4 The temporal evolution of solitary wave overtopping volume

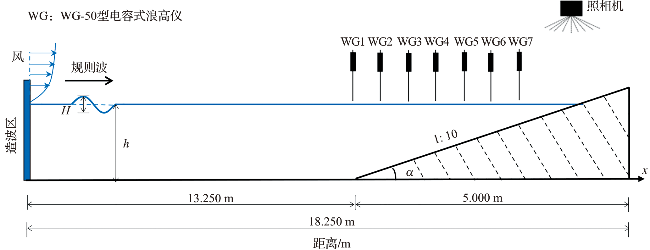
2.2 风影响下规则波传播变形的验证

为验证数值模型计算风对波浪传播变形的准确性,与JIANG 等[28]的物理模型实验结果进行对比(图5)。模型水槽长45.000 m,宽0.800 m,高1.000 m,斜坡坡度为1∶10,距造波边界13.250 m。每间隔0.600 m布设一个测点,共布设7个测点,第一个测点布设在坡脚处。实验中规则波的波高H为0.07 m,入射波周期T为1.5 s,静止水深h为0.40 m,恒定风速Uw为5.0 m·s-1。不同测点处数值模拟的波高时程曲线与实验数据的对比结果(图6)显示,数值计算结果与实验数据吻合较好,该数值模型可用于计算风对波浪传播变形的影响。
图5 实验区域布置图[28]

Fig.5 Experimental layout[28]

图6 不同测点处的波高时程曲线

Fig.6 The temporal evolution of wave height for different wave gauges

3 工况设置与结果分析

主要考虑向岸风风速( U w *)、入射波高(H)、堤顶超高(AC)、岸滩坡度(cotα)以及海堤坡度(cotβ)等5个因素对孤立波海堤越浪特性的影响。数值计算所采用的模型参考HUNT[11]的物理模型,如图7所示。数值计算的区域长28.330 m、高3.000 m。静止水深为0.50 m,将静止水深到海堤堤顶的高度定义为堤顶超高。在造波区上方输入恒定的风速,无量纲化后 U w *=Uw/ g h。当孤立波在斜坡式海堤上传播时,孤立波会发生不同类型的破碎,GRILLI 等[29]提出采用无量纲参数S0来划分孤立波的破碎类型:
S0=1.521 t a n α H / h
图7 计算区域布置图

Fig.7 Computational layout

当S0<0.025时,表示为激破波;当0.025<S0<0.300时,表示为卷破波;当0.300<S0<0.370时,表示为崩破波;当S0>0.370时,表示为非破碎波。表1表示数值计算的工况以及不同工况设置下的孤立波的破碎类型:在岸滩坡度cotα=10时,孤立波的破碎类型为激破波,其它工况的孤立波破碎类型均为卷破波。
表1 数值模拟工况和波浪破碎类型

Tab.1 Parameter setup of numerical simulation and wave breaking types

工况 U w * H/m AC/m cotα cotβ 破碎类型 工况 U w * H/m AC/m cotα cotβ 破碎类型
1 0 0.10 0.117 20 2 卷破波 23 4 0.10 0.067 20 2 卷破波
2 1 0.10 0.117 20 2 卷破波 24 0 0.10 0.117 10 2 激破波
3 2 0.10 0.117 20 2 卷破波 25 4 0.10 0.117 10 2 激破波
4 3 0.10 0.117 20 2 卷破波 26 0 0.10 0.117 15 2 卷破波
5 4 0.10 0.117 20 2 卷破波 27 4 0.10 0.117 15 2 卷破波
6 5 0.10 0.117 20 2 卷破波 28 0 0.10 0.117 20 2 卷破波
7 6 0.10 0.117 20 2 卷破波 29 4 0.10 0.117 20 2 卷破波
8 0 0.05 0.117 20 2 卷破波 30 0 0.10 0.117 25 2 卷破波
9 4 0.05 0.117 20 2 卷破波 31 4 0.10 0.117 25 2 卷破波
10 0 0.10 0.117 20 2 卷破波 32 0 0.10 0.117 30 2 卷破波
11 4 0.10 0.117 20 2 卷破波 33 4 0.10 0.117 30 2 卷破波
12 0 0.15 0.117 20 2 卷破波 34 0 0.10 0.117 20 0 卷破波
13 4 0.15 0.117 20 2 卷破波 35 4 0.10 0.117 20 0 卷破波
14 0 0.20 0.117 20 2 卷破波 36 0 0.10 0.117 20 1 卷破波
15 4 0.20 0.117 20 2 卷破波 37 4 0.10 0.117 20 1 卷破波
16 0 0.10 0.217 20 2 卷破波 38 0 0.10 0.117 20 2 卷破波
17 4 0.10 0.217 20 2 卷破波 39 4 0.10 0.117 20 2 卷破波
18 0 0.10 0.167 20 2 卷破波 40 0 0.10 0.117 20 3 卷破波
19 4 0.10 0.167 20 2 卷破波 41 4 0.10 0.117 20 3 卷破波
20 0 0.10 0.117 20 2 卷破波 42 0 0.10 0.117 20 4 卷破波
21 4 0.10 0.117 20 2 卷破波 43 4 0.10 0.117 20 4 卷破波
22 0 0.10 0.067 20 2 卷破波

3.1 水动力特性分析

有、无向岸风对孤立波海堤越浪的水动力特性有一定的影响。计算工况设置为:无量纲风速 U w *=0和 U w *=4,入射波高H=0.10 m,堤顶超高AC=0.117 m,岸滩坡度cotα=20,海堤坡度cotβ=2。图8表示有风和无风时不同时刻孤立波越浪的速度云图。由于向岸风的存在,波面存在小幅度的振荡,孤立波波峰处出现相比无风时更大的高速流动的水体区域(图8a和8b);当孤立波传播至海堤附近时,由于水深的减小以及海堤的阻碍,波峰逐渐变陡,孤立波逐渐达到破碎的临界形态(图8c和8d);水面上方的风会引起剪切应力和水面压力不平衡,使孤立波的传播速度增大,因此孤立波越浪的时刻会稍微提前(图8e和8f);当孤立波越过海堤时,水体被分成两部分,一部分水体在岸滩上继续爬高,另一部分水体由于海堤的阻碍发生反射(图8g和8h)。有风时,孤立波会产生更大的越浪量,并且向岸风使水面两侧出现压差,海堤附近会出现水体低速流动区。图9表示有风和无风时孤立波爬高和越浪量的时程变化。有风和无风时,孤立波爬高和越浪量的时程曲线变化趋势是一致的,但有风时的最大爬高和最大越浪量会有所增大,相比无风情况分别增大约7.7%和7.5%,这是因为向岸风增大了水体的能量。图10表示有风和无风时孤立波冲击海堤的水平荷载和垂直荷载。有风时海堤的水平荷载的峰值略大于无风情况(图10a),这是因为向岸风增大了孤立波的传播速度,使水体的动能增大,会对海堤产生更大冲击。向岸风带走了水体上方部分的空气流,海堤上方附近出现负压区,海堤两侧压差逐渐增大,因此有风时海堤垂直荷载的峰值大于无风情况(图10b)。有风时,水平荷载增大约3.3%,垂直荷载增大约13.2%。图11表示有风和无风时沿程最大水位高程的空间分布。有风和无风时,沿程最大水位高程的变化趋势基本一致。在海堤附近,有风时的沿程最大水位高程要略大于无风情况,这是因为向岸风增大了孤立波的波陡,使越浪的水体量增多。图12表示有风和无风时的湍流剪切应力。向岸风的存在使正湍流剪切应力明显增强,负湍流剪切应力明显减小。
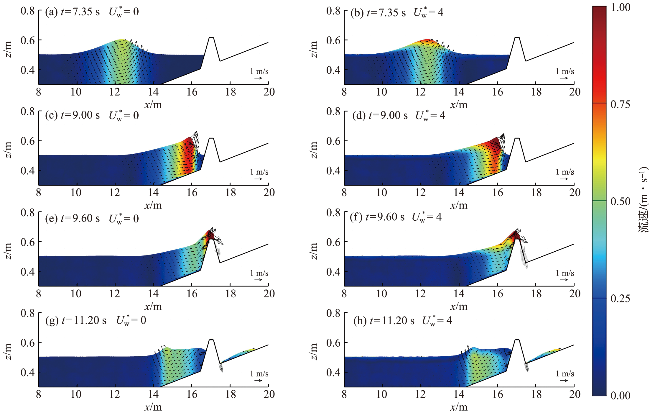
图8 有风和无风时不同时刻水体的速度云图

Fig.8 Velocity contours of water body at different time moments in windy and windless conditions

图9 有风和无风时孤立波爬高(a)和越浪量(b)时程曲线对比

Fig.9 Comparison of the time series of solitary wave runup height (a) and volume of overtopping water (b) in windy and windless conditions

图10 有风和无风时海堤所受的水动力荷载

Fig.10 Hydrodynamic forces exerted at the seawall in windy and windless conditions

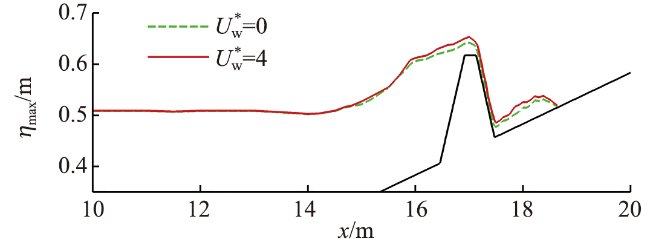
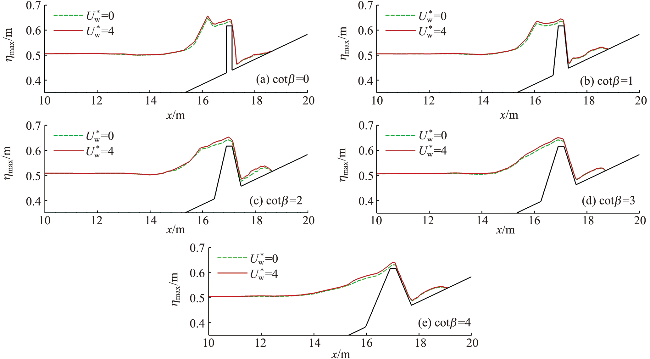
图11 有风和无风时沿程最大水位高程空间分布

Fig.11 Spatial distributions of the maximum water elevation in windy and windless conditions

图12 有风(a)和无风(b)时的湍流剪切应力对比

Fig.12 Comparison of turbulent shear stress between windy (a) and windless (b) conditions

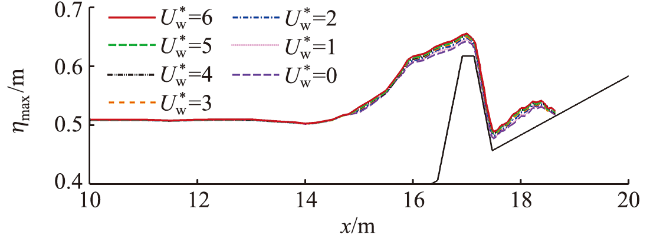
3.2 风速的影响

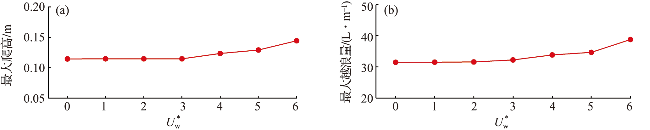
风速对孤立波海堤越浪的水动力特性有一定的影响。计算工况设置为:无量纲风速 U w *=0、1、2、3、4、5和6,入射波高H=0.10 m,堤顶超高AC=0.117 m。图13表示不同风速下孤立波的最大爬高和最大越浪量。当 U w *<2时,风对孤立波在斜坡式海堤上的最大爬高和最大越浪量影响不大;当 U w *>2时,随着风速的增大,最大爬高和最大越浪量逐渐增大,当 U w *从3增加到6时,最大爬高和最大越浪量分别增大约25.8%和22.7%。图14表示不同风速下不同测点处相对波高Hi/h(Hi表示波浪传播到不同位置处的波高)的比较。当孤立波在平底区域传播时,不同风速下的相对波高基本不变;当孤立波向岸滩上传播时,波形变陡,相对波高会有所增大;当波浪向海堤附近传播时,波浪破碎,相对波高迅速减小,这是因为波浪破碎后,部分能量被消耗,并且随风速的增大,相对波高稍稍增大。图15表示不同风速下沿程最大水位高程的空间分布。当波浪在平底区传播时,风速对沿程最大水位高程的影响不大;当波浪传播至海堤附近时,沿程最大水位高程随着风速的增大逐渐增大;当风速 U w *=6时,最大水位高程相比无风情况增大约2.07%。
图13 不同风速下孤立波的最大爬高(a)和最大越浪量(b)

Fig.13 Maximum runup height (a) and maximum overtopping volume (b) of solitary wave under different onshore wind speeds

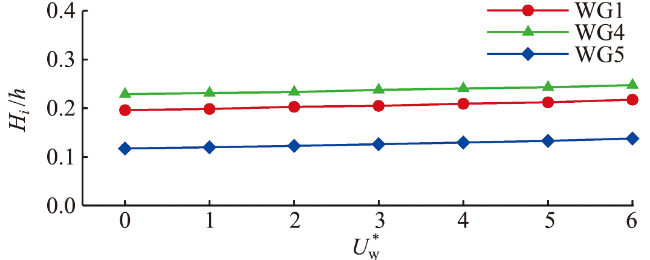
图14 不同风速下不同测点处相对波高的比较

Fig.14 Comparison of relative wave height for different wave gauges under different onshore wind speeds

图15 不同风速下沿程最大水位高程空间分布

Fig.15 Spatial distributions of the maximum water elevation under different onshore wind speeds

3.3 入射波高的影响

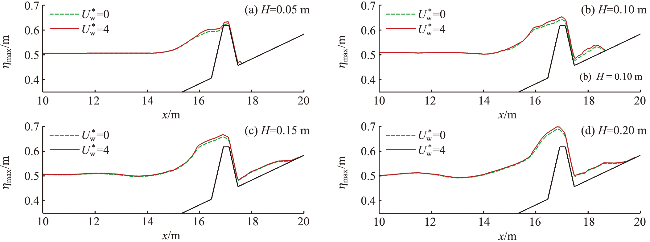
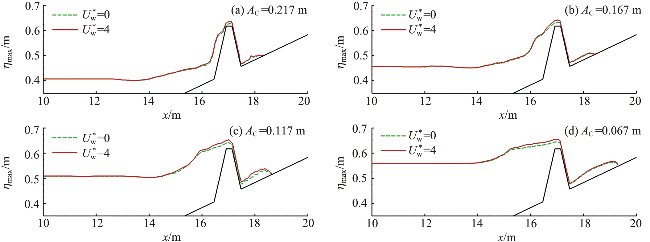
研究不同入射波高条件下孤立波海堤越浪的水动力特性,计算工况设置为:无量纲风速 U w *=0和 U w *=4,入射波高H分别为0.05、0.10、0.15和0.20 m,波高比H/h=0.10、0.20、0.30和0.40,堤顶超高AC=0.117 m。图16表示不同入射波高下有风和无风时孤立波的最大爬高和最大越浪量。随着入射波高的增大,孤立波的最大爬高和最大越浪量呈线性增长,当波高比H/h从0.10增加到0.40时,有风时孤立波的最大爬高和最大越浪量相比无风情况平均要增大约10.3%和3.9%。图17表示不同入射波高下有风和无风时不同测点处相对波高的比较。随入射波高的增大,不同测点处的相对波高差别逐渐增大。当波浪破碎后,相对波高迅速减小,这种破碎现象在相对波高比较大时更为明显。图18表示在不同入射波高下有风和无风时沿程最大水位高程的空间分布。随着入射波高的增大,沿程最大水位高程逐渐增大。在海堤附近,有风情况下沿程最大水位高程要比无风情况大,这是因为向岸风使波浪与海堤之间的非线性作用增强,相对波高会有所增大。
图16 不同入射波高下有风和无风时孤立波的最大爬高(a)和最大越浪量(b)

Fig.16 Maximum value of runup height (a) and maximum overtopping volume (b) of solitary wave in windy and windless conditions under different incident wave heights

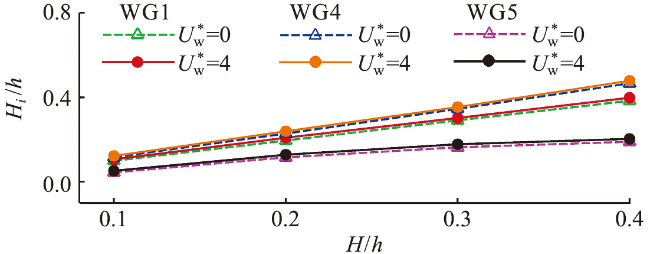
图17 不同入射波高下有风和无风时不同测点处相对波高的比较

Fig.17 Comparison of relative wave height for different wave gauges in windy and windless conditions under different incident wave heights

图18 不同入射波高下有风和无风时沿程最大水位高程空间分布

Fig.18 Spatial distributions of the maximum water elevation in windy and windless conditions under different incident wave heights

3.4 堤顶超高的影响

研究不同堤顶超高下孤立波在斜坡式海堤上越浪的水动力特性,计算工况设置为:无量纲风速 U w *=0和 U w *=4,入射波高H=0.10 m,堤顶超高AC分别为0.217、0.167、0.117和0.067 m,则无量纲堤顶超高 A C *=AC/H=2.17、1.67、1.17和0.67。图19表示不同堤顶超高( A C *=AC/H)下有风和无风时孤立波的最大爬高和最大越浪量。随堤顶超高的减小,孤立波的最大爬高和最大越浪量逐渐增大。在不同堤顶超高下,有风时孤立波的最大爬高和最大越浪量总比无风情况要大。平均而言,有风情况下的孤立波最大爬高和最大越浪量要比无风时分别增大约4.0%和15.9%。图20表示不同堤顶超高下有风和无风时不同测点处相对波高的比较。当孤立波在平底区传播时,不同堤顶超高条件下的相对波高基本不变;当孤立波传播至岸滩处,随着堤顶超高的减小,相对波高逐渐减小,这是因为堤顶超高越小,波浪发生浅化破碎的作用越弱;当孤立波传播至海堤附近时,随着堤顶超高的减小,相对波高会逐渐增大,这是因为堤顶超高越小,波浪破碎损失的能量越少。图21表示不同堤顶超高下有风和无风时沿程最大水位高程的空间分布。随堤顶超高的减小,沿程最大水位高程逐渐增大。当波浪传播至海堤附近时向岸风的影响逐渐增大,沿程最大水位高程相比无风时会增大。
图19 不同堤顶超高下有风和无风时孤立波的最大爬高(a)和最大越浪量(b)

Fig.19 Maximum value of runup height (a) and maximum overtopping volume (b) of solitary wave in windy and windless conditions under different dimensionless crest freeboards

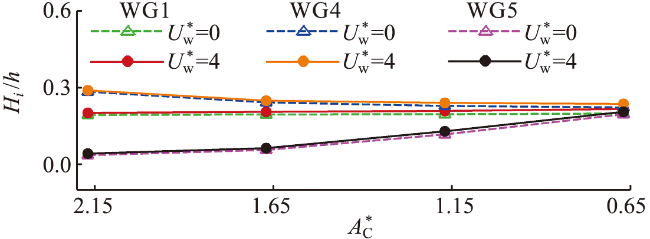
图20 不同堤顶超高下有风和无风时不同测点处相对波高的比较

Fig.20 Comparison of relative wave height for different wave gauges in windy and windless conditions under different dimensionless crest freeboards

图21 不同堤顶超高下有风和无风时沿程最大水位高程空间分布

Fig.21 Spatial distributions of the maximum water elevation in windy and windless conditions under different dimensionless crest freeboards

3.5 岸滩坡度的影响

研究不同岸滩坡度对孤立波海堤越浪的水动力特性的影响,计算工况设置为:无量纲风速 U w *=0和 U w *=4,入射波高H=0.10 m,堤顶超高AC=0.117 m,5种岸滩坡度cotα=10、15、20、25和30。图22表示不同岸滩坡度下有风和无风时孤立波的最大爬高和最大越浪量。孤立波的最大爬高和最大越浪量随岸滩坡度的增大单调增大,有风时孤立波的最大爬高和最大越浪量都要比无风时大。平均而言,有风时的孤立波最大爬高和最大越浪量要比无风时分别增大约4.9%和8.8%。图23表示不同岸滩坡度下有风和无风时不同测点处相对波高的比较。当孤立波在平底区传播时,不同岸滩坡度下的相对波高变化不大;当波浪传播至岸滩处,随着岸滩坡度的增大,相对波高逐渐减小;当波浪传播至海堤附近时,随着岸滩坡度的增大,相对波高逐渐增大。图24表示不同岸滩坡度下有风和无风时沿程最大水位高程的空间分布。随着岸滩坡度的增大,海堤附近的沿程最大水位高程逐渐减小,这是因为越过海堤上方的水体逐渐减少。
图22 不同岸滩坡度下有风和无风时孤立波的最大爬高(a)和最大越浪量(b)

Fig.22 Maximum value of runup height (a) and maximum overtopping volume (b) of solitary wave in windy and windless conditions under different beach slopes

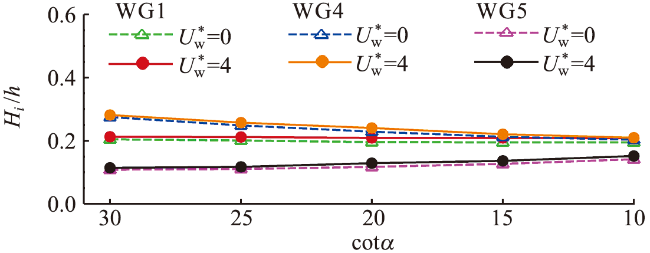
图23 不同岸滩坡度下有风和无风时不同测点处相对波高的比较

Fig.23 Comparison of relative wave height for different wave gauges in windy and windless conditions under different beach slopes

图24 不同岸滩坡度下有风和无风时沿程最大水位高程空间分布

Fig.24 Spatial distributions of the maximum water elevation in windy and windless conditions under different beach slopes

3.6 海堤坡度的影响

研究不同海堤坡度对孤立波海堤越浪水动力特性的影响,计算工况设置为:无量纲风速 U w *=0和 U w *=4,入射波高H=0.10 m,堤顶超高AC=0.117 m,5种不同的海堤坡度cotβ=0、1、2、3和4。图25表示不同海堤坡度下有风和无风时孤立波的最大爬高和最大越浪量。除cotβ=0的海堤结构以外,随着海堤坡度的增大,孤立波的最大爬高逐渐增大,最大越浪量单调递减。向岸风会增强波浪的的水动力特性,使孤立波的最大爬高和最大越浪量增大,平均而言,孤立波的最大爬高和最大越浪量相比无风情况分别增大约4.9%和8.1%。图26表示不同海堤坡度下有风和无风时不同测点处相对波高的比较。海堤坡度的改变对孤立波在平底区和岸滩位置处的相对波高影响不大;当波浪传播至海堤附近时,随着海堤坡度的增大,相对波高逐渐增大,这是因为海堤坡度越大,波浪越容易发生破碎。图27表示不同海堤坡度下有风和无风时沿程最大水位高程的空间分布。随着海堤坡度的逐渐增大,沿程最大水位高程逐渐增大;当孤立波传播至海堤附近时,向岸风对沿程最大水位高程的影响逐渐显现,有风时的沿程最大水位高程相比无风时要大。
图25 不同海堤坡度下有风和无风时孤立波的最大爬高(a)和最大越浪量(b)

Fig.25 Maximum value of runup height (a) and maximum overtopping volume (b) of solitary wave in windy and windless conditions under different seawall slopes

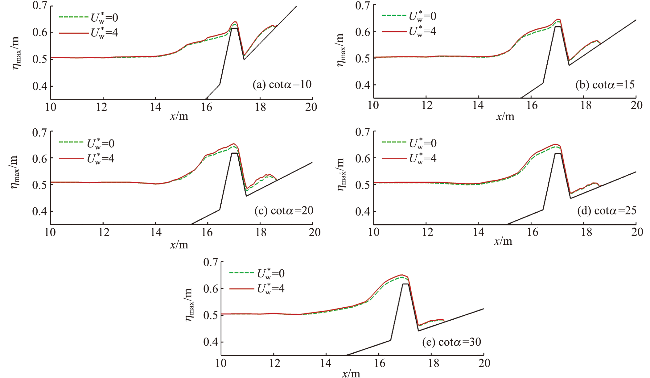
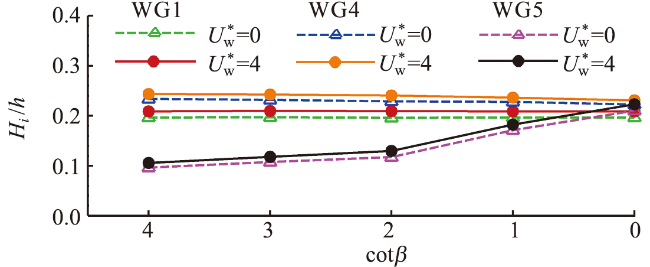
图26 不同海堤坡度下有风和无风时不同测点处相对波高的比较

Fig.26 Comparison of relative wave height for different wave gauges in windy and windless conditions under different seawall slopes

图27 不同海堤坡度下有风和无风时沿程最大水位高程空间分布

Fig.27 Spatial distributions of the maximum water elevation in windy and windless conditions under different seawall slopes

4 结论

基于二维不可压缩两相流数值模型对风影响下孤立波海堤越浪的水动力特性进行分析,考虑向岸风的风速( U w *)、入射波高(H)、堤顶超高(AC)、岸滩坡度(cotα)和海堤坡度(cotβ)等5个不同因素的影响,主要结论如下。
1)有向岸风时,孤立波越浪的水动力特性更为显著,孤立波水体高速流动区域明显增大,破碎时刻和破碎位置均会提前,在海堤上更早地发生越浪过程。
2)随着向岸风风速的增大,孤立波波峰水体流速会增大,孤立波在斜坡式海堤上的最大爬高、最大越浪量以及沿程最大水位高程均有所增大。
3)随着入射波高的增大和堤顶超高的减小,孤立波的最大爬高、最大越浪量以及沿程最大水位高程逐渐增大。
4)随着岸滩坡度的增大,孤立波在岸滩上损失的能量减少,最大爬高、最大越浪量均有所增大。
5)随着海堤坡度的增大(除cotβ=0外),孤立波的最大爬高和最大越浪量分别增大和减小。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
CHO Y S, PARK K Y, LIN T H. Run-up heights of nearshore tsunamis based on quadtree grid system[J]. Ocean Engineering, 2004, 31(8/9): 1093-1109.

DOI

[2]
SYNOLAKIS C E, BERNARD E N. Tsunami science before and beyond Boxing Day 2004[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2006, 364(1845): 2231-2265.

DOI

[3]
姚远, 蔡树群, 王盛安. 海啸波数值模拟的研究现状[J]. 海洋科学进展, 2007, 25(4):487-494.

YAO Y, CAI S Q, WANG S A. Present status of study on numerical simulation of tsunami wave[J]. Advances in Marine Science, 2007, 25(4): 487-494.

[4]
QU K, REN X Y, KRAATZ S. Numerical investigation of tsunami-like wave hydrodynamic characteristics and its comparison with solitary wave[J]. Applied Ocean Research, 2017, 63: 36-48.

DOI

[5]
SATO S, OKAYASU A, YEH H, et al. Delayed survey of the 2011 Tohoku tsunami in the former exclusion zone in Minami-soma, Fukushima Prefecture[J]. Pure and Applied Geophysics, 2014, 171(12): 3229-3240.

DOI

[6]
HARINARAYANA T, HIRATA N. Destructive earthquake and disastrous tsunami in the Indian Ocean, what next?[J]. Gondwana Research, 2005, 8(2): 246-257.

DOI

[7]
MORI N, TAKAHASHI T. The 2011 Tohoku earthquake tsunami joint survey group. Nationwide post event survey and analysis of the 2011 Tohoku earthquake tsunami[J]. Coastal Engineering Journal, 2012, 54(1): 1250001.

[8]
QUIROGA P D, CHEUNG K F. Laboratory study of solitary-wave transformation over bed-form roughness on fringing reefs[J]. Coastal Engineering, 2013, 80: 35-48.

DOI

[9]
YAO Y, HE F, TANG Z J, et al. A study of tsunami-like solitary wave transformation and run-up over fringing reefs[J]. Ocean Engineering, 2018, 149: 142-155.

DOI

[10]
DE WAAL J P, VAN DER MEER J W. Wave runup and overtopping on coastal structures[C]// American Society of Civil Engineers, Coastal Engineering, 1992, 1993: 1758-1771.

[11]
HUNT A. Extreme waves, overtopping and flooding at sea defences[D]. Oxford: University of Oxford, 2003.

[12]
HSIAO S C, LIN T C. Tsunami-like solitary waves impinging and overtopping an impermeable seawall: Experiment and RANS modeling[J]. Coastal Engineering, 2010, 57(1): 1-18.

DOI

[13]
LIN T C, HWANG K S, HSIAO S C, et al. An experimental observation of a solitary wave impingement, run-up and overtopping on a seawall[J]. Journal of Hydrodynamics, 2012, 24(1): 76-85.

DOI

[14]
张金牛, 吴卫, 刘桦, 等. 孤立波作用下斜坡堤越浪量的实验研究[J]. 水动力学研究与进展A辑, 2014, 29(6):656-662.

ZHANG J N, WU W, LIU H, et al. An experimental study on overtopping of solitary wave against a slope dike[J]. Journal of Hydrodynamics, 2014, 29(6): 656-662.

[15]
曾婧扬, 吴卫, 刘桦. 孤立波斜坡堤堤顶及后坡越浪流数值分析[J]. 力学季刊, 2013, 34(2):181-190.

ZENG J Y, WU W, LIU H. Numerical analysis of overtopping flow on crest and landward slope of seadike in solitary wave[J]. Chinese Quarterly of Mechanics, 2013, 34(2): 181-190.

[16]
王键, 孙大鹏, 吴浩. 带胸墙斜坡堤越浪量的数值试验研究[J]. 海洋工程, 2018, 36(4):138-146.

WANG J, SUN D P, WU H. Numerical study on overtopping of sloping breakwater with crown-wall[J]. The Ocean Engineering, 2018, 36(4): 138-146.

[17]
万德成, 戴世强. 孤立波与潜水台阶相互作用的数值模拟[J]. 水动力学研究与进展A辑, 1998, 13(1):95-100.

WAN D C, DAI S Q. Numerical study of the interaction between a solitary wave and a submerged step obstacle[J]. Chinese Journal of Hydrodynamics, 1998, 13(1): 95-100.

[18]
万德成, 缪国平. 数值模拟波浪翻越直立方柱[J]. 水动力学研究与进展A辑, 1998, 13(3):363-370.

WAN D C, MIAO G P. Numerical simulations of waves overtopping an erect quadrate column[J]. Chinese Journal of Hydrodynamics, 1998, 13(3): 363-370.

[19]
QU K, WEN B H, REN X Y, et al. Numerical investigation on hydrodynamic load of coastal bridge deck under joint action of solitary wave and wind[J]. Ocean Engineering, 2020, 217: 108037.

DOI

[20]
WEN B H, QU K, LAN G Y, et al. Numerical study on hydrodynamic characteristics of coastal bridge deck under joint action of regular waves and wind[J]. Ocean Engineering, 2022, 245: 110450.

DOI

[21]
GUO L, QU K, HUANG J X, et al. Numerical study of influences of onshore wind on hydrodynamic processes of solitary wave over fringing reef[J]. Journal of Marine Science and Engineering, 2022: 10: 1645.

[22]
KUNDU P K, COHEN I M, DOWLING D R. Fluid mechanics[M]. Academic Press, 2015.

[23]
ISSA R I. Solution of the implicitly discretised fluid flow equations by operator-splitting[J]. Journal of Computational Physics, 1986, 62(1): 40-65.

DOI

[24]
FERZIGER J H, PERIĆ M. Computational methods for fluid dynamics[M]. 3rd, rev. ed. Berlin: Springer 2002.

[25]
JASAK H. Error analysis and estimation for the finite volume method with applications to fluid flows[D]. London, UK: Imperial College London, 1996.

[26]
RHIE C M, CHOW W L. Numerical study of the turbulent flow past an airfoil with trailing edge separation[J]. AIAA Journal, 1983, 21(11): 1525-1532.

DOI

[27]
WILCOX D C. Turbulence modeling for CFD[M]. 2nd ed. La Canada, Calif.: DCW Industries, 1998.

[28]
JIANG C B, YANG Y, DENG B. Study on the nearshore evolution of regular waves under steady wind[J]. Water, 2020, 12(3): 686.

DOI

[29]
GRILLI S T, SVENDSEN I A, SUBRAMANYA R. Breaking criterion and characteristics for solitary waves on slopes[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1997, 123(3): 102-112.

DOI

Options
Outlines

/

〈 〉