Journal of Marine Sciences >

2024 , Vol. 42 >Issue 2: 81 - 90

DOI: https://doi.org/10.3969/j.issn.1001-909X.2024.02.008

Data processing method and application of towed marine three-component magnetic gradiometer

  • DANG Lingfeng 1 ,
  • WU Zhaocai 1, 2, * ,
  • DONG Chongzhi 1 ,
  • ZHANG Jialing 1, 3
Expand
  • 1. Second Institute of Oceanography, Key Laboratory of Submarine Geosciences, MNR, Hangzhou 310012, China
  • 2. School of Surveying, Mapping and Spatial Information, Shandong University of Science and Technology, Qingdao 266590, China
  • 3. Oceanography Institute, Zhejiang University, Zhoushan 316021, China

Received date: 2023-04-12

  Revised date: 2023-05-27

  Online published: 2024-08-09

Fold

Abstract

The towed marine three-component magnetic gradiometer can obtain the geomagnetic three-component and magnetic gradient data at the same time. Compared with the traditional towed geomagnetic total field magnetometer, the towed marine three-component magnetic gradiometer has the advantages of reducing the ship magnetic interference and resisting the influence of geomagnetic daily variation, but it also has some shortcomings such as sensitivity error, zero offset error, orthogonality error and position error. In the actual voyage, a section data measured by the towed marine three-component magnetic gradiometer was calibrated to the total geomagnetic field data measured by the G880 magnetometer, which proved its high stability and reliability. Based on the three component magnetic gradient data, the tensor invariants and the trend of magnetic boundary were obtained, and combined with the Euler deconvolution calculation, the magnetic source body on the measurement line was effectively identified and interpreted. The results show that the towed three-component marine gradiometer can effectively obtain the information of geomagnetic field, component and gradient, which can provide a more effective technical means for marine geomagnetic field measurement.

Key words： geomagnetic three components; calibration of scalar; magnetic gradient tensor; magnetic boundary trend map; Euler deconvolution

Cite this article

DANG Lingfeng , WU Zhaocai , DONG Chongzhi , ZHANG Jialing . Data processing method and application of towed marine three-component magnetic gradiometer[J]. Journal of Marine Sciences, 2024 , 42(2) : 81 -90 . DOI: 10.3969/j.issn.1001-909X.2024.02.008

0 引言

光泵磁力仪、质子磁力仪等传统的海洋磁力仪,测量的均是地磁场的标量,即对地磁总场进行测量,难以获得地磁场的梯度或分量等矢量信息。船载地磁三分量测量是利用三分量磁通门传感器测量得到地磁场分量、磁偏角等地磁场矢量信息,可成功地应用于地质解释[1⇓⇓⇓⇓⇓-7]。但船载地磁三分量测量受船体磁场干扰,海上现场校正过程比较复杂。拖曳式磁力仪是通过拖缆将磁力仪拖曳于距船尾超过三倍船长的海水中,减小了船体磁场的干扰。日本科学家SEAMA等[8]于1997年开发了用于深拖测量的矢量磁力仪,并在Nankai盆地进行了首次实验。美国斯克里普斯海洋研究所于 2002年研制了可以拖曳在测量船后方的三分量测磁系统,可以分辨30~50 nT以上的水平和垂直磁异常[9]。德国联邦地质与自然资源研究所和美国斯克里普斯海洋研究所合作开发了一套能够在10~12 kn船速下进行拖曳测量的矢量磁力仪系统[10]。除了拖曳式的海洋地磁三分量测量外,也可以采取类似于拖曳的地磁梯度测量方式[11]进行三分量磁力梯度测量,它可避免地磁日变对地磁测量的影响,并可同步获得地磁分量及磁力梯度信息。本文介绍了一种拖曳式海洋三分量磁力梯度仪,对测量的地磁三分量及梯度数据进行了处理,结果表明拖曳式海洋三分量磁力梯度测量能够获得比传统的地磁总场测量更多的地磁矢量信息,有效地反映了地壳内部地质体的磁属性,可为今后的海洋磁力测量提供更有效的技术手段。

1 数据来源和方法

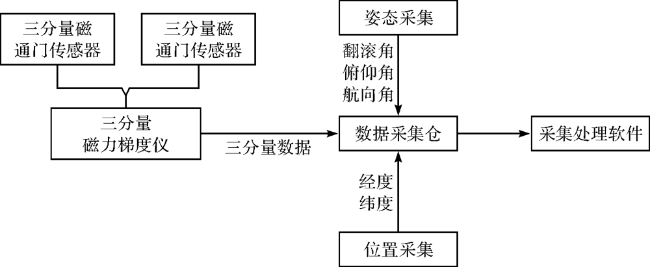
1.1 数据采集

本文使用的拖曳式海洋三分量磁力梯度仪是由自然资源部第二海洋研究所与中船重工第七一五所合作研发的一种新型海洋磁力仪,主要由水下拖体和甲板采集单元等两部分组成。水下拖体包含三分量磁通门传感器、姿态传感器和温度压力传感器等部分,用于测量地磁场的分量和梯度,拖体的姿态变化、入水深度和工作环境温度等参数。甲板采集单元包括数据采集仓和采集处理软件。数据采集仓接收由水下拖体采集的磁场、姿态角和船上的导航定位等综合信息,这些信息经同步处理后连接到采集处理软件,校正处理后进行显示和存储(图1为测量系统的数据采集流程图)。与常见的总场磁力仪相比,拖曳式海洋三分量磁力梯度仪能够同时获得地磁三分量与梯度数据,能够有效降低船磁干扰和抵抗地磁日变影响,通过姿态仪可以实时监控拖体在水中的姿态变化,减少因姿态变化对磁测数据产生的影响,使用简单、高效、成本低。
图1 数据采集流程图

Fig.1 Flow chart of data acquisition

2021年,“大洋号”科考船在海底地震仪(ocean bottom seismometer,OBS)炸测作业的走航过程中,利用拖曳式海洋三分量磁力梯度仪在印度洋莫桑比克海域采集了一条近东西走向,长约528 km的测线(图2)。作业时使用了300 m长的拖缆,拖曳深度在25~30 m之间,船速约为5.5 kn,采样间隔为0.2 s。采用了滤波和去噪等数据处理方法以减少环境影响对实测数据的干扰。
图2 测线位置示意图

Fig.2 Sketch map of survey line location

1.2 数据处理

1.2.1 单个三分量磁通门传感器的校准

三分量磁通门传感器的三个轴理论上应该是相互正交且完全相同的。由于生产工艺水平的限制,三个轴存在正交性误差、灵敏度误差和零点偏移误差。针对单个的三分量磁通门传感器,误差模型校准已有成熟方法,正交性误差、灵敏度误差和零点偏移误差与三分量磁力仪针对载体磁干扰的标量校准方法相类似[5,12⇓-14]。
假设一个理想的正交系统坐标系为O0X0Y0Z0,三个轴的输出值分别为x0、y0、z0,三分量磁通门传感器的实际坐标系为O1X1Y1Z1,对应的输出值为x1、y1、z1。每个轴的实际输出值都可以用理想输出值的三个分量在实际坐标轴上的投影相加得到。假定将实际坐标系与理想坐标系的Z轴重合,其余实际坐标轴与理想坐标轴的夹角分别为α、β、γ。在实际情况中,这些坐标轴的夹角通常在1°以内,所以cosα≈1、cosβ≈1、cosγ≈1、sinα≈α、sinβ≈β、sinγ≈γ。正交性误差矩阵可以简化为S= 1 γ α 0 1 β 0 0 1,假设传感器的灵敏度误差矩阵为K= k x 0 0 0 k y 0 0 0 k z,零点偏移误差矩阵为b= b x b y b z,这样可以得到磁感应强度实际输出值 f1与理想输出值 f0的关系:
f1=KSf0+b
f0=S-1·K-1f1-S-1·K-1b
由此,单个三分量磁通门传感器的校准就转化成了求解三个误差系数矩阵中九个未知数的问题。利用最小二乘法,测量N个数据得到N个方程组,当方程组的个数大于未知系数的个数时,就可以求得相应的正交性误差矩阵系数、灵敏度误差矩阵系数、零点偏移误差矩阵系数,进而得到校准后的三分量数据。

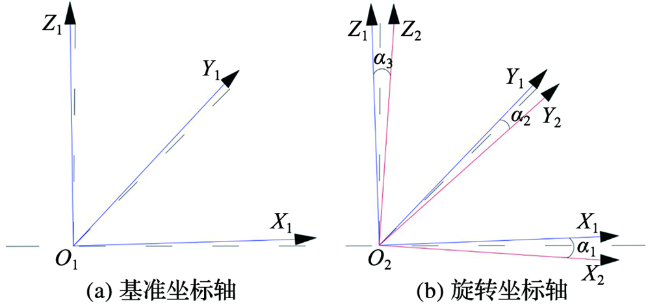
1.2.2 两个在三分量磁通门传感器的互校准

在拖曳式三分量磁力梯度测量系统中,两个三分量磁通门传感器的坐标系统由于安装工艺的限制并不能完全一一对应,存在较小角度的偏差,这就导致了位置误差的存在。可以通过坐标变换进行修正,即以其中一个传感器的坐标系为基准,通过旋转另一个传感器的坐标轴来实现坐标系的修正[15-16](图3)。
图3 坐标轴旋转示意图

(两个磁力传感器的坐标系分别为O1X1Y1Z1和 O 2 X 2Y2Z2,以 O 1 X 1Y1Z1坐标系为基准,三个旋转角分别为α1、α2、α3。图中虚线表示虚拟理想正交坐标轴。)

Fig.3 Schematic diagram of axis rotation

(The coordinate systems of the two magnetometers are O1X1Y1Z1 and O2X2Y2Z2, Based on the axes O1X1Y1Z1, the three rotation angles are α1,α2,α3. The dotted line is the virtual ideal orthogonal coordinate axis.)

位置误差本身是一个较小角度的偏差,三个旋转角也非常小,在1°以内,因此cosα1≈1、cosα2≈1、cosα3≈1、sinα1≈α1、sinα2≈α2、sinα3≈α3。可以得到三分量磁通门传感器测量的磁感应强度 f1和 f2的分量关系如下:
f x 1 ≈ f x 2 + α 3 f y 2 - α 2 f z 2 f y 1 ≈ - α 3 f x 2 + f y 2 + α 1 f z 2 f z 1 ≈ α 2 f x 2 - α 1 f y 2 + f z 2
f1和 f2的位置误差矩阵Dt为
Dt= 1 α 3 - α 2 - α 3 1 α 1 α 2 - α 1 1
由此,两个三分量磁通门传感器的位置误差校准问题就转化成了求解位置误差矩阵的问题。利用最小二乘法,测量N个数据得到N个方程组,当方程组的个数大于未知系数的个数时,通过方程组求解得到相应系数,进而得到校准后的地磁三分量和梯度数据。
在拖曳式三分量磁力梯度仪投入到海上实际测量之前,先在陆地上的无磁性实验室内对单个三分量磁通门传感器误差校正的9个系数和两个三分量磁通门传感器的位置误差校正的3个系数进行测定,根据测定后的系数,在采集过程中进行实时校正。

1.2.3 姿态校正

假设传感器的坐标轴系统与拖体坐标轴系统经校准后一致,在拖曳式三分量磁力梯度测量过程中,姿态仪实时采集拖体的姿态(包括航向角α、翻滚角β、俯仰角γ),并通过姿态角对拖体的坐标系统进行转换,将测量数据换算到地理坐标系中,从而进行实时输出。坐标转换公式为
fe=Dfs
式中: fe为地理坐标系下的磁感应强度; fs为拖体坐标系下的磁感应强度;D为转换矩阵,其表达式为
$\boldsymbol{D}=\left(\begin{array}{ccc} \cos \alpha \cos \gamma-\sin \alpha \sin \gamma \sin \beta & \sin \alpha \cos \gamma+\cos \alpha \sin \gamma \sin \beta & -\sin \gamma \cos \beta \\ -\sin \alpha \cos \beta & \cos \alpha \cos \beta & \sin \beta \\ \cos \alpha \cos \gamma+\sin \alpha \sin \gamma \sin \beta & \sin \alpha \cos \gamma-\cos \alpha \sin \gamma \sin \beta & \cos \gamma \cos \beta \end{array}\right)$
在实际采集过程中由于存在高频噪声和跳点,因此还需要进行高频滤波。前、后两个三分量磁通门传感器(T1和T2)测得的地磁X、Y、Z分量最终结果见图4,三个分量磁力梯度见图5。
图4 磁力传感器T1与T2的三分量磁感应强度数据

Fig.4 Three-component magnetic induction intensity data of magnetometer T1 and T2

图5 三分量磁力梯度数据

Fig.5 Three-component magnetic gradient data

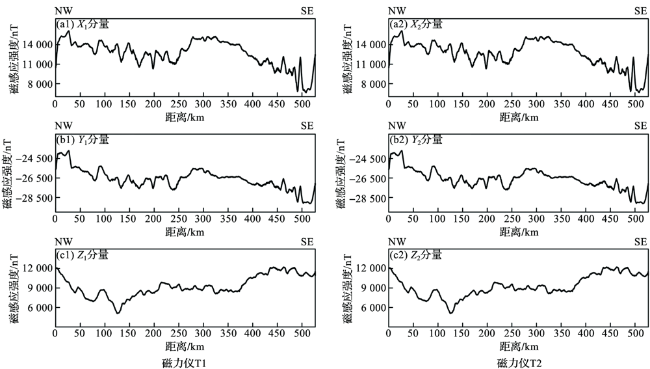
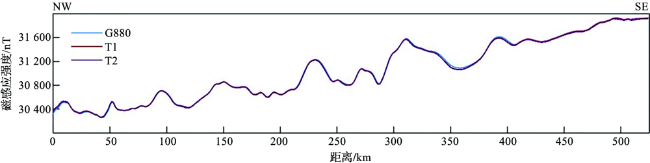
1.3 外符合精度评价

在拖曳式海洋三分量磁力仪测量的同一条测线上,用G880磁力仪重复测量地磁总场,根据黄谟涛 等[17]的外符合公式来计算拖曳式三分量磁力梯度仪测量数据的两个合成地磁总场与G880测量的地磁总场的符合精度,即外符合精度,计算公式为
ε=± ∑ j = 1 m ( ∑ i = 1 n δ i j 2 ) m × n
δij=Fij-Pi
式中: ε为外符合精度;Fij为第j条重复线第i点的观测值;Pi为第i点已知的外符合标准场值(i=1,2,3,…,n, j=1,2,3,…,m,), m为重复线的数目,n为重复线公共段数据点数;δij为Fij与Pi之差。
计算结果如图6所示,第一个合成的地磁总场与G880测量地磁总场的外符合精度为4.03 nT,第二个合成的地磁总场与G880测量地磁总场的外符合精度为5.51 nT。结果表明重复线测量精度良好,本次测量所用的拖曳式三分量磁力梯度仪工作状态良好,测量可信度较高。
图6 三分量磁力梯度仪合成的地磁总场与G880所测地磁总场对比

Fig.6 Comparison of three-component composite geomagnetic total field with that measured by G880

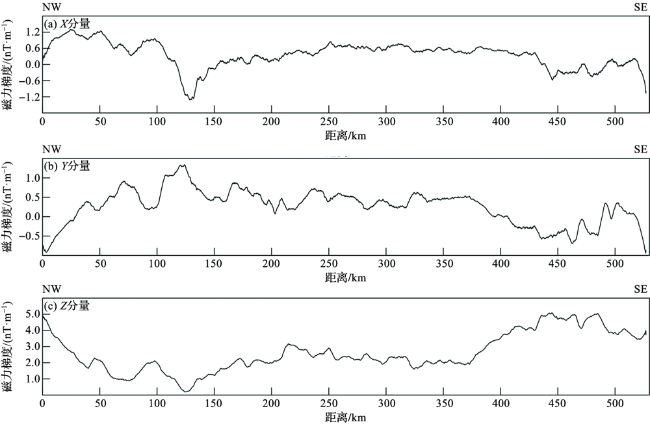
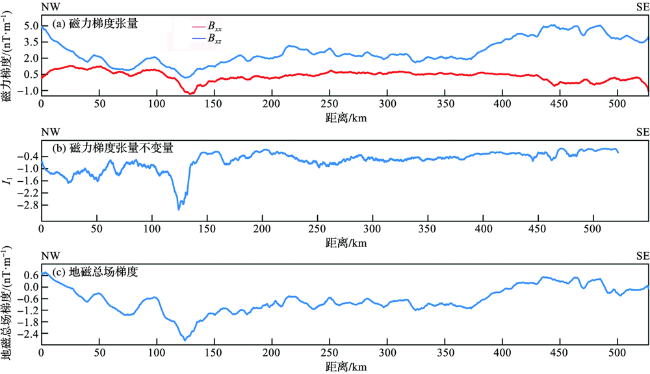
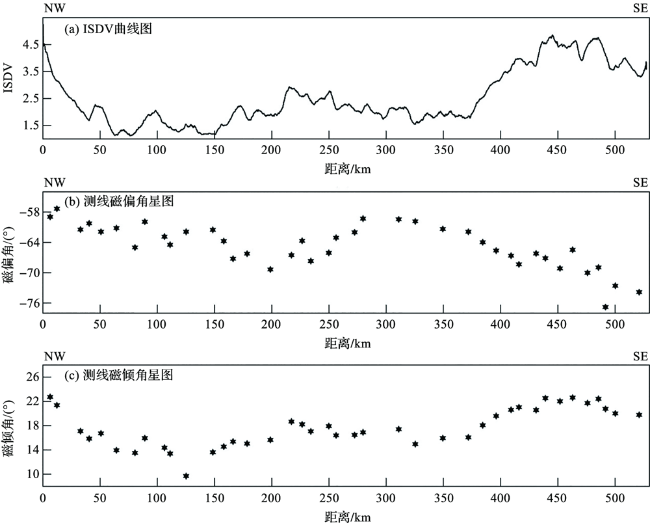
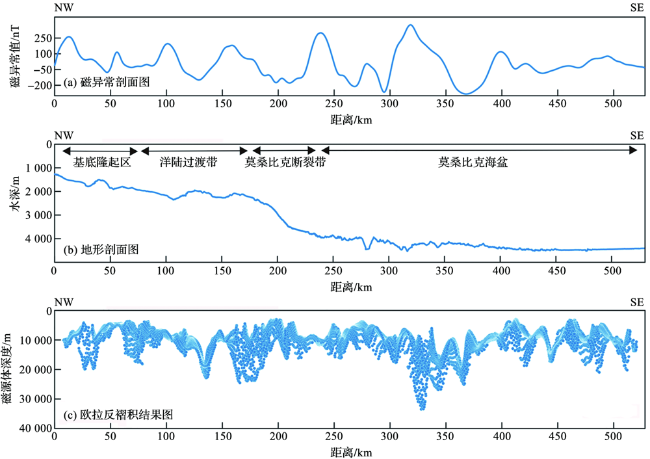
2 结果与分析

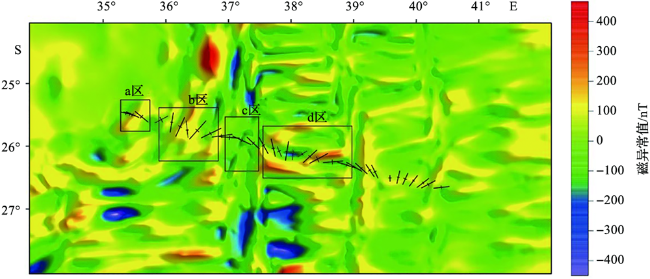
2.1 磁源体边界位置

本文所测的三分量磁力梯度数据有Bxx、Byx和Bzx三个张量,可以依据二维的磁力梯度张量计算其张量不变量[18],降低磁化方向变化对磁异常偏斜的影响,更好地指示磁源体位置。磁力梯度张量矩阵T的张量不变量计算公式[19]为
I1=det(T)=BxxBzz-BxzBzx
式中:Bxx为X分量水平磁力梯度;Bzx为Z分量水平磁力梯度;Bzz为 Z分量垂向磁力梯度;Bxz为X分量垂向磁力梯度;I1为磁力梯度张量不变量,为无量纲量(图7b)。
图7 磁力梯度张量(a)、磁力梯度张量不变量(b)与地磁总场梯度(c)对比图

Fig.7 The contrast diagram of magnetic gradient tensor (a), magnetic gradient tensor invariant (b) and total magnetic field gradient (c)

地磁总场梯度剖面曲线在磁源体边界会出现异常峰值,据此可以有效分辨磁源体的位置。利用测量得到的三分量磁力梯度数据合成的地磁总场梯度如图7c所示。
整体来看,地磁总场梯度范围在-2.76~0.73 nT/m之间,在剖面西北端约为0.73 nT/m,向东南方向逐渐减小,在125 km处出现最小值-2.76 nT/m,而后逐渐上升至-1.2 nT/m左右,在150~375 km之间,变化较缓,中间存在多处小峰值异常,然后开始上升,上升至0.2 nT/m后变化剧烈。Bxx、Bxz与磁力梯度张量不变量的曲线变化情况保持一致,磁力梯度变化剧烈的位置基本对应,磁力梯度变化最大处指示了洋陆边界的位置。
根据磁场理论,磁场的水平导数能够突出边界异常[7]。因此,计算空间差分矢量强度(intensity of the spatial differential vector,ISDV)可以得到磁源体边界位置,ISDV表达式为
$\left|\frac{\partial F}{\partial x}\right|=\sqrt{\left(\frac{\partial F_{x}}{\partial x}\right)^{2}+\left(\frac{\partial F_{y}}{\partial x}\right)^{2}+\left(\frac{\partial F_{z}}{\partial x}\right)^{2}}$
式中: ∂ F ∂ x即表示ISDV,为无量纲量;Fx、Fy、Fz分别表示地磁场的北向、东向和垂向分量。
根据计算结果画出ISDV曲线图(图8a),其中每一个峰值都对应一个可能的磁边界。根据实际情况计算图中峰值所对应的磁偏角和磁倾角(图8b、图8c)。
图8 ISDV曲线与测线磁倾角、磁偏角对比图

Fig.8 Comparison diagram of ISDV curve with magnetic inclination angle and magnetic declination angle of measured line

为了进一步直观地判断磁源体边界的位置,根据磁边界走向图(magnetic boundary strike diagram,MBSD)法[6],对三分量磁力梯度数据进行处理,得到了综合直观的磁边界走向图(图9)。
图9 磁边界走向图

(图中黑色线段的中心点对应磁边界的位置;长线段的方向对应磁边界的磁偏角,线段长度与磁边界磁倾角的余弦值成正比;短线段的长度与磁边界矢量的标准差成正比。)

Fig.9 Strike diagram of magnetic boundary

(The central point of the black line segment in the figure corresponds to the position of the magnetic boundary. The direction of the long line segment corresponds to the magnetic declination angle of the magnetic boundary, and the length of the line segment is proportional to the cosine value of the magnetic inclination angle of the magnetic boundary. The length of the short line segment is proportional to the standard deviation of the magnetic boundary vector.)

从图9可以看出,磁源体边界的位置和走向与测区磁异常走向特征基本吻合,结合磁力梯度张量不变量和地磁总场梯度的变化情况,可以得到磁异常分区: a区位于北纳塔尔裂谷,区域内的磁源体边界集中分布在一个正磁异常附近;b区位于莫桑比克海脊,磁源体边界沿区域内一个近南北走向的线性高磁异常均匀分布;c区位于莫桑比克断裂带,磁源体边界的位置和方向比较杂乱,与该处大规模的断层活动有关;d区位于莫桑比克海盆,磁源体边界的位置和方向与该区域中心的负磁异常对称分布。

2.2 欧拉反褶积

欧拉反褶积方法能在先验信息较少的情况下自动或半自动地确定磁场源位置,有效地推算出磁源体的位置和深度[20]。首先对合成地磁总场进行地磁正常场改正,求得磁异常数据[21⇓-23](图10a),而后进行二维欧拉反褶积计算,计算公式如下:
(x-x0) ∂ T ∂ x-z0 ∂ T ∂ z=-NT(x)
式中:N为构造指数,取为1;坐标(x0,z0)为等效源点相对于剖面的深度和位置; ∂ T ∂ x、 ∂ T ∂ z分别为磁异常数据的水平方向导数和垂直方向导数;T(x)为磁异常值。
图10 磁异常剖面(a)、地形剖面(b)与欧拉反演结果(c)对比图

Fig.10 Comparison diagram of magnetic anomaly profile (a), topographic profile (b) and Euler inversion results (c)

实测测线横跨莫桑比克南部陆缘(图2),区域岩浆活动强烈,经历了多次构造运动,地壳构造复杂,是板块构造的活跃带之一[24-25]。测线近东西走向,依次经过北纳塔尔裂谷、莫桑比克海脊、莫桑比克断裂带至莫桑比克海盆。结合该区域的地震剖面[26],以基底变形特征、岩浆活动情况对照磁力梯度张量不变量和磁边界走向图的变化特征,可将该区域大致分为基底隆起区、洋陆过渡带、莫桑比克断裂带和莫桑比克海盆区四部分(图10b)。
基底隆起区磁异常范围在-90~260 nT之间,从45 km处开始,磁场正负伴生,变化剧烈(图10a),欧拉反褶积结果显示,存在欧拉解浅部聚集(图10c),对应海底地形出现隆起(图10b),推测可能为浅部岩浆磁源体的反映。
洋陆过渡带存在大规模火山沉积地层,局部地区发育向海倾斜的反射层,是富岩浆型大陆边缘的标志[25]。该区的磁异常范围在-148~200 nT之间,130 km处出现幅值为-148 nT的负磁异常,欧拉解也出现 ‘V’ 型下切态势(图10c)。在此区域莫霍面迅速抬升,地壳厚度减薄[26],磁力梯度张量及不变量也表现为负峰值,推测该处为显著的磁性构造边界。
莫桑比克断裂带呈南北向分布,是冈瓦纳大陆沿转换断层走滑形成的,断裂带基底变形严重,为莫桑比克南部陆缘与莫桑比克海盆的分界线[25]。该区的磁异常在-178~280 nT之间,地形总体呈现先降低而后变化平缓的特征。欧拉反褶积结果显示,该处存在大量欧拉解聚集,聚集范围深度超过8 km,宽度超过50 km(图10c),表明可能存在与断裂带相关的大规模磁源物质。
莫桑比克海盆区磁异常范围在-283~375 nT之间,在320 km左右达到峰值,400 km后,磁异常曲线变化变缓。欧拉反褶积结果也显示,在320 km左右出现规模和深度较大的欧拉解聚集区(图10c),可能反映了莫桑比克断裂带向莫桑比克海正常洋壳过渡中复杂的磁性物质变化。

3 结论

根据在莫桑比克南部陆缘采集到的拖曳式海洋地磁三分量和磁力梯度剖面数据,经过传感器校准和姿态校正,计算了磁力梯度张量不变量和空间差分矢量,得到了相应的磁边界走向图,并利用三分量磁力梯度数据计算了欧拉反褶积,据此分析了莫桑比克南部陆缘磁源体的边界位置和变化情况。主要结论如下。
1)使用G880磁力仪的测量结果与拖曳式海洋三分量磁力梯度仪合成的地磁总场进行外符合精度评价,外符合精度分别为4.03 nT和5.51 nT,表明本次使用的拖曳式海洋三分量磁力梯度仪具有良好的稳定性和可行性。
2)基于地磁总场梯度、磁力梯度张量及其张量不变量,结合磁边界走向图和地质构造背景,确定了洋陆边界的位置,即磁力梯度张量不变量剖面曲线变化最大处。
3)基于莫桑比克南部陆缘海域的磁异常数据的欧拉反褶积结果和地磁异常特征认为,洋陆过渡带区域存在显著的磁性构造边界,莫桑比克断裂带区域存在与断裂带相关的大规模磁源物质,反映了莫桑比克断裂带向莫桑比克海正常洋壳过渡中复杂的磁性物质变化。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
ISEZAKI N, MATSUDA J I, INOKUCHI H, et al. Shipboard measurement of three components of geomagnetic field[J]. Journal of Geomagnetism and Geoelectricity, 1981, 33(5): 329-333.

[2]
ISEZAKI N. A new shipboard three-component magnetometer[J]. Geophysics, 1986, 51(10): 1992-1998.

[3]
LEE S M, KIM S S. Vector magnetic analysis within the southern Ayu Trough, equatorial Western Pacific[J]. Geophysical Journal International, 2004, 156(2): 213-221.

[4]
KATO H, ISEZAKI N, PARK C H, et al. Characteristics of crustal magnetic structures in the Tsushima (Ulleung) and Japan Basins from vector magnetic anomalies[J]. Earth, Planets and Space, 2007, 59(7): 887-895.

[5]
王文健, 高金耀, 吴招才, 等. 南极普里兹湾船载地磁三分量数据处理分析[J]. 极地研究, 2017, 29(3):349-356.

WANG W J, GAO J Y, WU Z C, et al. Processing and analyses on shipboard three-component magnetometer data from Prydz Bay, Antarctica[J]. Chinese Journal of Polar Research, 2017, 29(3): 349-356.

[6]
赵俊峰. 南海北部海盆三分量磁测结果分析[J]. 热带海洋学报, 2009, 28(4):54-58.

ZHAO J F. Analysis of three-component magnetic data from northern South China Sea Basin[J]. Journal of Tropical Oceanography, 2009, 28(4): 54-58.

[7]
SEAMA N, NOGI Y, ISEZAKI N. A new method for precise determination of the position and strike of magnetic boundaries using vector data of the geomagnetic anomaly field[J]. Geophysical Journal International, 1993, 113(1): 155-164.

[8]
SEAMA N, YAMAMOTO M, ISEZAKI N. A newly developed deep tow three component magnetometer[J]. Eos, 1997, 78(46): 192.

[9]
GEE J S, CANDE S C. A surface-towed vector magnetometer[J]. Geophysical Research Letters, 2002, 29(14): 1670.

[10]
ENGELS M, BARCKHAUSEN U, GEE J S. A new towed marine vector magnetometer: Methods and results from a Central Pacific cruise[J]. Geophysical Journal International, 2008, 172(1): 115-129.

[11]
徐行, 龚跃华, 王功祥, 等. 海洋磁力梯度测量技术在水合物勘探中的应用[J]. 海洋地质与第四纪地质, 2005, 25(3):97-101.

XU X, GONG Y H, WANG G X, et al. Application of the marine magnetic gradient measurements to the exploration of gas hydrate[J]. Marine Geology & Quaternary Geology, 2005, 25(3): 97-101.

[12]
闫辉, 肖昌汉, 沈明, 等. 船载地磁场三分量测量算法的实验验证[J]. 海洋测绘, 2010, 30(3):27-29.

YAN H, XIAO C H, SHEN M, et al. The algorithm verification for geomagnetic three-component computation with shipboard measurement system[J]. Hydrographic Surveying and Charting, 2010, 30(3): 27-29.

[13]
周超烨, 金际航, 李宏武, 等. 三分量磁通门传感器校正的循环优化算法[J]. 海洋测绘, 2010, 30(4):63-66,72.

ZHOU C Y, JIN J H, LI H W, et al. Repeat-optimization algorithm for the calibration of triaxial fluxgate magnetometers[J]. Hydrographic Surveying and Charting, 2010, 30(4): 63-66, 72.

[14]
BRONNER A, MUNSCHY M, SAUTER D, et al. Deep-tow 3C magnetic measurement: Solutions for calibration and interpretation[J]. Geophysics, 2013, 78(3): J15-J23.

[15]
高翔, 严胜刚, 李斌. 三轴磁通门磁梯度仪转向差校正方法研究[J]. 仪器仪表学报, 2016, 37(6):1226-1232.

GAO X, YAN S G, LI B. Study on the steering differential calibration method for magnetic gradiometer base on tri-axis fluxgate[J]. Chinese Journal of Scientific Instrument, 2016, 37(6): 1226-1232.

[16]
高翔, 严胜刚, 李斌. 基于最小二乘的磁通门梯度仪转向差校正方法[J]. 西北工业大学学报, 2016, 34(5):837-842.

GAO X, YAN S G, LI B. Error calibration method for magnetic gradiometer base on least square[J]. Journal of Northwestern Polytechnical University, 2016, 34(5): 837-842.

[17]
黄谟涛, 欧阳永忠, 翟国君, 等. 海面与航空重力测量重复测线精度评估公式注记[J]. 武汉大学学报:信息科学版), 2013, 38(10):1175-1177.

HUANG M T, OU-YANG Y Z, ZHAI G J, et al. Comment on the formulas of accuracy evaluation for multi-line overlapping measurements in ship-borne and airborne gravity survey[J]. Geomatics and Information Science of Wuhan University, 2013, 38(10): 1175-1177.

[18]
吴招才. 磁力梯度张量技术及其应用研究[D].武汉:中国地质大学, 2008.

WU Z C. Magnetic gradient tensor technology and its application[D]. Wuhan: China University of Geoscience, 2008.

[19]
徐熠. 磁梯度张量异常反演算法与算例[D]. 北京: 中国地质大学(北京), 2015.

XU Y. Inversion of magnetic gradient tensor and example[D]. Beijing: China University of Geosciences, 2015.

[20]
PERMANA N R, GUNAWAN B, PRIMASTIKA AA, et al. Characteristics of Palu-Koro Fault based on derivative analysis and Euler deconvolution model of gravity data[J]. Journal of Physics: Conference Series, 2022, 2377(1):012041.

[21]
孙中任, 赵雪娟, 王丽娜. 地面磁测数据正常场改正现行方法探讨[J]. 地质与勘探, 2011, 47(4):679-685.

SUN Z R, ZHAO X J, WANG L N. Discussion of current correction methods of the normal magnetic field for data processing of ground magnetic surveys[J]. Geology and Exploration, 2011, 47(4): 679-685.

[22]
简燕, 李文尧, 武中华. 高精度磁测正常场改正和高度改正精度[J]. 物探与化探, 2011, 35(3):368-370,387.

JIAN Y, LI W Y, WU Z H. A discussion on normal field correction and altitude correction of high-precision magnatic survey[J]. Geophysical and Geochemical Exploration, 2011, 35(3): 368-370, 387.

[23]
ALKEN P, THÉBAULT E, BEGGAN C D, et al. Interna-tional geomagnetic reference field: the thirteenth generation[J]. Earth, Planets and Space, 2021, 73(1): 49.

[24]
HANYU T, NOGI Y, FUJII M Crustal formation and evolution processes in the Natal Valley and Mozambique Ridge, off South Africa[J]. Polar Science, 2017, 13: 66-81.

[25]
WATREMEZ L, LEROY S, D’ACREMONT E, et al. The Limpopo magma-rich transform margin, South Mozambique: 1. insights from deep-structure seismic imaging[J]. Tectonics, 2021, 40(12): e2021TC006915.

[26]
李赫. 转换型大陆边缘地壳结构及构造-沉积演化过程研究:以东非莫桑比克南部陆缘为例[D].杭州:浙江大学, 2021.

LI H Crustal architecture and tectonic-sedimentary evolution of the transform continental margin[D].Hangzhou: Zhejiang University, 2021.

Options
Outlines

/

〈 〉