Journal of Marine Sciences >

2024 , Vol. 42 >Issue 3: 108 - 118

DOI: https://doi.org/10.3969/j.issn.1001-909X.2024.03.009

Prediction of sea level changes along the coast of China using machine learning models

  • CHEN Jianheng ,
  • XU Dongfeng , * ,
  • YAO Zhixiong
Expand
  • State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography,MNR, Hangzhou 310012, China

Received date: 2023-11-23

  Revised date: 2024-01-30

  Online published: 2024-11-25

Fold

Abstract

Based on the data of satellite altimetry and six tide gauge stations along the coast of China, linear regression function was used to estimate the absolute sea level rise rate in the coastal areas of China from 1993 to 2020, which was 4.17±1.32 mm/a, and the relative sea level rise rate was 4.47±0.90 mm/a. Taking the atmospheric data, ocean data and climate modal index from 1958 to 2020 as prediction factors, a variety of neural network models such as long short-term memory neural network model (LSTM model), recurrent neural network model (RNN model), gated recurrent unit neural network model (GRU model) and support vector machine regression model (SVR model) were established to predict the trend of relative sea level changes around the six tide gauge stations along the coast of China. The model evaluation results show that the average correlation coefficient and root mean square error of the observed value and the predicted value obtained by the LSTM model that simultaneously introduces atmospheric and ocean variables and climate modal index variables are 0.866 and 19.279 mm, respectively, which performs the best among the four models, and therefore the LSTM model can be used as a new method for predicting relative sea level changes.

Key words： sea level rise; relative sea level; absolute sea level; vertical land movement; satellite altimetry; tide level; LSTM neural network model; time series forecasting

Cite this article

CHEN Jianheng , XU Dongfeng , YAO Zhixiong . Prediction of sea level changes along the coast of China using machine learning models[J]. Journal of Marine Sciences, 2024 , 42(3) : 108 -118 . DOI: 10.3969/j.issn.1001-909X.2024.03.009

0 引言

近年来全球变暖问题日益突出,海平面上升是全球变暖的一个重要指标[1-2]。随着格陵兰岛和南极洲等陆基冰盖的融化,预计海平面上升趋势将会增大。从验潮仪和卫星测高观测得到的全球平均海平面上升速率从1901—1990年期间的1.4 mm/a增加到1993—2015年期间的3.2 mm/a,再到2006—2015年期间的3.6 mm/a。预计到2100年,全球平均海平面相对于1986—2005年的将上升0.43~0.84 m[3]。
中国沿海海平面变化总体呈加速上升趋势[4],1980—2022年平均上升速率为3.5 mm/a,1993—2022年平均上升速率为4.0 mm/a,高于同时段全球平均水平[5]。海平面变化在时间和空间上存在差异,其影响和风险也存在差异,人口密度高、海拔低、地面沉降率高、适应能力弱的沿海地区承受能力最差。因此,准确预测沿海海平面变化对于沿海地区防灾减灾至关重要[3]。
海平面变化受到许多因素影响,除了受到与气候变化因素有关的长期变化趋势影响外,还受到年际和年代际气候变化趋势影响。年际和年代际变化趋势受到海水热膨胀和盐度变化(比容效应)、气压和风、陆地和海洋冰融化、海洋环流、河流径流等影响的同时,也受到厄尔尼诺-南方涛动(El Niño-Southern Oscillation,ENSO)、北大西洋涛动(North Atlantic Chronological Oscillation,NAO)、太平洋年代际振荡(Pacific Decadal Oscillation,PDO)或北太平洋涡旋振荡(North Pacific Gyre Oscillation,NPGO)等气候模态影响,从而引起大规模海平面变化[1,6⇓⇓⇓-10]。季节性沿海海平面变化还会受到潮汐和各种水文气象过程的动态影响。例如,在威灵顿地区,海面温度、海面盐度和平均海平面压力等海洋参数已被确定为海平面变化的主要驱动因素[11]。而在红海地区,则是气温、风速、云量和蒸发速率等大气参数对当地海平面变化起主要作用。在红海地区的人工神经网络海平面预测模型中加入云量作为预报因子后发现,云量异常与海平面异常具有良好的相关性,模型取得了良好的预测效果[12]。在研究沿海海平面变化时,地壳垂直运动和气候变化一样值得重视[6,13-14]。因为在海平面绝对上升的同时,由于地壳垂直运动,海平面还存在着相对上升。
近年来,随着数据数量和质量的提高以及计算机技术的进步,已有许多方法用于沿海海平面变化预测。其中,数值模式适用于全球和区域海平面的长期预测,但用于预测沿海海平面变化需要大量的海洋和大气数据以及大量计算资源[15-16],因过于复杂而不适用。潮汐分析对于模拟由短期天文潮汐引起的海平面变化非常有效,但对于长时间序列的预测作用很小[11]。差分整合移动平均自回归模型(autoregressive integrated moving average model,ARIMA)等经典时间序列模型虽被广泛应用于海平面变化研究,但这些模型使用简单的线性关系,无法捕捉海洋-大气过程的非线性复杂特征[14]。深度学习等人工智能(artificial intelligence,AI)技术已成为模拟海平面变化的有效替代方案。许多人工神经网络(artificial neural networks,ANN)和循环神经网络(recurrent neural networks,RNN)已经在实际研究中得以使用[11⇓⇓-14]。长短期记忆神经网络(long-short term memory,LSTM)在时间序列预测方面具有独特性能,可通过增加记忆单元里的控制门来解决RNN模型短期记忆的问题。LSTM的复杂架构可以允许长时间存储之前输入的层信息,并允许将其运用到后续的训练中,从而高效地处理长时间序列信息,实现对复杂函数的建模。因此,LSTM的应用越来越普遍[17-18]。
验潮仪在海平面监测中发挥着重要作用。从验潮仪记录中获得的海平面被称为相对海平面,能够表征一定区域内的沿海海平面,其中包含了由于气候变化(如海洋升温、陆地冰融化或水质量重新分布等)和地壳垂直运动(如冰川均衡调整、构造运动、沉积物压实、地下水耗竭、修建大坝或填埋场沉降等)引起的验潮仪记录数据的变化[19⇓⇓⇓⇓⇓-25]。自1993年以来,一系列测高卫星提供了几乎所有海洋不受地壳垂直运动影响的海面高度高精度测量数据,成为研究全球平均海平面变化和沿海地区的绝对海平面变化的重要数据[26⇓-28]。有学者通过验潮仪研究了中国不同沿海地区的相对海平面[29⇓⇓⇓-33],也有学者利用卫星测高数据研究了中国海域的区域极端海平面变化[34⇓⇓-37],但迄今为止很少有人同时使用验潮仪数据和卫星测高数据并结合机器学习方法对中国沿海的海平面变化进行研究。考虑到卫星具有全天时、全天候的连续数据获取能力,而机器学习方法具有能够高效处理大批量数据的优势,本文利用1993—2020年中国海域6个验潮站及测高卫星的长期观测资料,分析了中国沿海绝对海平面和相对海平面的上升趋势,并结合卫星测高资料对中国沿海的地壳垂直运动趋势进行了分析,最后建立了多种神经网络模型预测中国沿海海平面变化,并且评估出了最优预测模型。

1 研究方法

1.1 循环神经网络

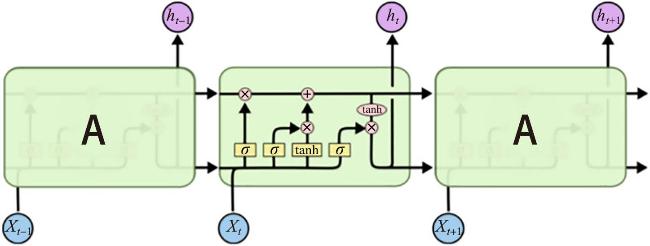
RNN是一类特殊的神经网络,主要用于处理文本、语音、时间等序列数据。与传统的前馈神经网络不同,RNN可以通过循环连接来处理序列数据中的时序信息。
RNN的基本结构是一个循环单元,它包括一个输入、一个输出以及一个隐藏状态。RNN的输入是当前时刻的输入数据以及上一时刻的隐藏状态;输出是当前时刻的输出数据以及当前时刻的隐藏状态。通过这种循环连接方式,RNN可以在处理序列数据时保留历史信息,并利用历史信息来影响当前时刻的输出和隐藏状态。

1.2 长短期记忆神经网络

LSTM在本质上是RNN的改进版本,与RNN最大的区别是增加了三个逻辑控制单元(即控制门,包括输入门、输出门和遗忘门)来解决RNN的短期记忆问题,通过改变神经网络的记忆单元与其他部分连接的权值大小来控制信息流的输入、输出以及记忆单元的状态[38]。其中输入门用于控制信息是否能够被记录到记忆单元中;输出门用于控制当前时间节点记忆单元中的信息是否能够流入到当前隐藏层中;遗忘门用于选择性遗忘上一时刻记忆单元的信息并累加到当前时刻记忆单元中[39]。图1为LSTM模型结构示意图,其中Xt为当前状态下数据的输入,Xt-1和Xt+1分别是上一时刻和下一时刻的输入数据,ht为当前隐藏层,ht-1和ht+1分别是上一时刻和下一时刻的隐藏层,A表示一个记忆细胞,σ和tanh为当前记忆单元中两个不同的激活函数,“×”和“+”分别代表矩阵相乘和矩阵相加运算。
图1 LSTM模型结构示意图

Fig.1 Schematic diagram of LSTM model structure

在LSTM的训练过程中,首先把t时刻的数据特征信息输入到输入层中,经过激活函数得到输出结果;然后将输出结果、t-1时刻的记忆单元存储信息和t-1时刻隐藏层输出结果输入到当前LSTM结构处理单元中,通过三个控制门的处理后,输出结果将进入下一输出层和隐藏层;最后计算反向传播误差,更新各个递归连接权重的大小。在t时刻LSTM每个记忆单元中的数据处理过程如下:
ft=σ(Wf·[ht-1,xt]+bf)
it=σ(Wi·[ht-1,xt]+bi)
ot=σ(Wo·[ht-1,xt]+bo)
C ̄ t=tanh(Wc·[ht-1,xt]+bc)
Ct=ft×Ct-1+it× C ̄ t
ht=ot×tanh(Ct)
式中: ft、it、ot分别指遗忘门、输入门和输出门;Wf、Wi、Wo分别代表了其对应的控制门的递归连接权重;bf、bi、bo是对应控制门的误差值;xt代表当前时刻的输入信息;ht代表t时刻隐藏层的输出值,ht-1代表上一时刻隐藏层的输出值;Ct-1代表上一时刻神经元记忆状态的记忆单元,Ct代表当前神经元记忆状态的记忆单元,具有随着训练不断地存储、读取、重置和更新长时间信息的能力, C ~ t表示记忆单元状态更新值;Wc表示记忆单元状态更新的权重矩阵;bc表示记忆单元状态更新的误差值。控制门结构由激活函数与点乘组成,公式中的激活函数σ在0~1之间取值,tanh在-1~1之间取值。点乘决定了记忆单元可以传送的信息量。激活函数的计算公式如下:
σ(x)= 1 1 + e - x
tanh(x)= e x - e - x e x + e - x

1.3 门控循环单元神经网络

门控循环单元神经网络(gate recurrent unit,GRU)是RNN的一种。和LSTM一样,GRU也是为了解决长期记忆和反向传播中的梯度等问题而提出来的。LSTM具有更长的记忆能力,在大部分序列任务上面都取得了比基础的RNN更好的性能表现,更重要的是,LSTM不容易出现梯度爆炸现象。但是LSTM结构相对较复杂,计算代价较高,模型参数量较大。在GRU中只有两个门(更新门和重置门),节约了计算资源,因此在众多的简化版LSTM中,GRU应用广泛。

1.4 支持向量机回归

支持向量机算法是机器学习里监督学习的一种分类算法,可以用作回归,即支持向量机回归(support vector regression,SVR)。SVR是通过寻找最小的结构化风险来改进学习机的泛化能力,将结果的经验风险和置信区间控制在最小范围,从而使人工神经网络在统计样本量较少的情况下也可以有效获取良好的统计规律。

1.5 超参数搜索

在机器学习过程中需要对超参数进行优化,给模型选择一组最优超参数,以提高学习的性能和效果。选择合适的超参数对于神经网络的训练至关重要。然而,人工调参效率过低。本研究采用随机超参数搜索策略,相较于网格搜索和人工调参,该方法能够节省计算资源、提高学习效率,并且可在连续且更大的范围内进行搜索。对于学习率、隐藏层节点数和批大小这样的连续型超参数,宜在连续分布的空间内取样进行设置[40]。

1.6 准确性评估

本文利用相对海平面异常预测值与验潮站记录的潮位异常时间序列的均方根误差(root mean square error,RMSE)和皮尔逊相关系数(Pearson correlation coefficient,PCC),评价模型预测值的准确性:
R M S E = 1 n ∑ i = 1 n ( x i - y i ) 2
P C C = ∑ i = 1 n ( x i - x ¯ ) ( y i - y ¯ ) ∑ i = 1 n ( x i - x ¯ ) 2 ∑ i = 1 n ( y i - y ¯ ) 2
式中:xi={x1,x2,…xn}为潮位异常预测值, x ¯为潮位异常预测值的平均值,yi={y1,y2,…yn}为潮位异常观测值, y ¯为潮位异常观测值的平均值。

1.7 垂直地壳运动趋势估计

对验潮站的月平均海平面数据进行预处理得出相对海平面异常,以估计相对海平面变化趋势;从卫星测高数据中提取验潮站位置的绝对海平面异常,以估计绝对海平面变化趋势。根据WÖPPELMANN等[41]结合验潮仪和卫星测高数据估计地壳垂直运动趋势的方法确定所有验潮站的绝对海平面(ASL)、相对海平面(RSL)以及地壳垂直运动(VLM)的变化趋势,它们之间的关系如下:
ASL=RSL+VLM

2 数据及模型介绍

2.1 数据介绍

平均海平面长期服务(Permanent Service for Mean Sea Level,PSMSL,https://psmsl.org/)公开数据中中国海岸线上的验潮站有6个(表1),本文选择了这6个验潮站1993—2020年的长期观测数据来分析海平面变化。这6个验潮站的月平均海平面异常(sea level anomaly,SLA)数据从哥白尼海洋环境监测服务(Copernicus Marine Environment Monitoring Service,CMEMS,https://data.marine.copernicus.eu/products)获得。
表1 研究使用的验潮站位信息

Tab.1 Informations of tide gauge stations used in this research

站点 站点号 起始
年份		 纬度/(°N) 经度/(°E) 1993—2020年
数据完整度/%
大连 723 1954年 38.867 121.683 98.5
吕四 979 1961年 32.133 121.617 87.7
坎门 934 1959年 28.083 121.283 97.6
大埔滘 1034 1963年 22.442 114.184 98.8
闸坡 933 1959年 21.583 111.817 98.8
西沙 1745 1990年 16.833 112.333 98.8
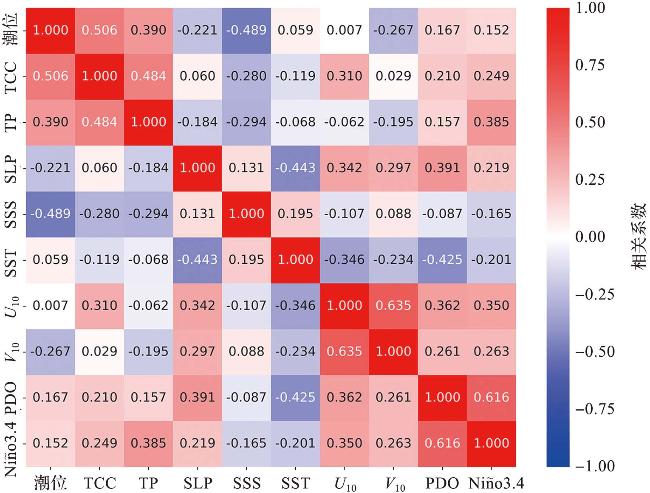
用于机器学习的数据主要包括以下几部分:一是美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration, NOAA)基于第五代版本ERSST(extended reconstruction sea surface temperature)扩展重建的PDO指数和Niño3.4指数数据;二是ERA5(ECMWF reanalysis v5)再分析数据集提供的总云量、降水、海平面气压、海面温度、海面10 m纬向风速及10 m经向风速数据;三是ORA5(Ocean Reanalysis System 5)再分析数据集中的海面盐度数据。这三部分数据的时间范围统一为1958—2020年。为计算相对海平面高度异常时间序列并与绝对海平面高度异常数据进行对比,将相对海平面高度减去的长期平均值取值范围定为1993—2012年,除PDO指数及Niño3.4指数外的其余数据异常值计算也做此处理。由于本文引入的PDO指数和Niño3.4指数在季节内信号不明显,但对年际至年代际事件有重要影响,也为了消除短期极端天气事件及极端数据影响,利用巴特沃斯滤波器对所有数据进行1年低通滤波处理,让模型更好地学习相对海平面的年际变化特征。

2.2 预报因子的选取

计算所有变量之间的相关性,进行相关分析,确定训练模型的最佳特征变量作为预报因子。选取出的预报因子有大气变量:总云量(total cloud cover,TCC)、总降水量(total precipitation,TP)、海平面气压(sea level pressure,SLP)、海面10 m经向风速(V10)和纬向风速(U10);海洋变量:海面温度(sea surface temperature,SST)和海面盐度(sea surface salnity,SSS);气候模态指数变量:PDO指数和Niño3.4指数。上述预报因子与坎门验潮站观测潮位的相关系数矩阵如图2所示。由图可知除海面温度和纬向风速外,其他预报因子与潮位的相关性系数均大于0.15。但是考虑到海温与纬向风速对海平面的影响具有确切的物理机制,并且海平面变化对其产生响应具有一定时间上的滞后,也将它们选作预报因子。
图2 坎门验潮站预报因子与潮位的相关系数矩阵

Fig.2 Correlation coefficient matrix between forecast factors and tide level at Kanmen tidal gauge station

2.3 模型训练与调参

在各验潮站分别建立多变量模型,并将海洋变量、大气变量及气候模态指数用于模型输入。为了确定最优网络结构,先进行预训练。以LSTM模型为例,预训练过程中输入变量数为9,设置LSTM层神经元个数为150,学习率大小为0.000 1,批大小为100,输入变量的时间序列数据长度为384。
每个站点的预测目标数据包含336个样本,首先确定最佳的训练集与验证集比例。本文采用递增时间窗交叉验证法对模型进行交叉验证[42],使用RMSE评估模型的准确性[43],结果如表2所示。由表可知,按9∶1的比例划分数据集训练的模型预测性能最优,故采用9∶1的比例划分LSTM模型数据集,即89%的数据(1993—2017年的300个样本)用于训练,11%的数据(2018—2020年的36个样本)用于验证,并设置无验潮站记录的潮位异常的预测时间长度与验证集的相同(2021—2023年的36个预测值),其他模型参照此比例。
表2 不同数据集划分比例的预训练结果准确性评估

Tab.2 Accuracy evaluation of pre-training results with different data set division ratios

数据集划分比例(训练集∶验证集) 归一化RMSE PCC
5∶5 0.415 0.309
6∶4 0.325 0.460
7∶3 0.214 0.739
8∶2 0.108 0.828
9∶1 0.095 0.839
根据大气变量、海洋变量和气候模态指数变量的预报因子构成,将模型输入变量组合分为7种场景,从中找出最佳变量组合。以LSTM模型为例,输入层的单位被设置为各个场景中的变量数量:场景1为2个,用OV(ocean variables)表示;场景2为5个,用AV(atmospheric variables)表示;场景3为2个,用IV(index variables)表示;场景4为7个,用OAV(ocean & atmospheric variables)表示;场景5为4个,用OIV(ocean & index variables)表示;场景6为7个,用AIV(atmospheric & index variables)表示;场景7为9个,用OAIV(ocean-atmospheric & index variables)表示。
基于RMSE和PCC评价标准的7个多变量场景的LSTM模型性能评估(表3)显示:用海洋变量训练的模型比用大气变量训练的模型的RMSE低,而用气候模态指数变量训练的模型比用海洋变量训练的模型的RMSE更低,这表明气候模态与海洋过程比大气过程对模型性能的影响更大,这与前人研究发现的“ENSO对中国沿海海平面年际变化有着重要的影响,在厄尔尼诺事件形成和发展过程中,东亚及西太平洋海平面明显下降”[1,3]很好地对应。在7种变量组合训练的LSTM模型中,输入OAIV变量组合进行训练的LSTM模型PCC最大,RMSE最小,性能最优,之后使用这个变量组合对模型进行训练。
表3 坎门验潮站不同输入变量组合下LSTM模型预训练结果的准确性评估

Tab.3 Accuracy evaluation of pre-training results of LSTM model with different input variable combinations for Kanmen tidal gauge station

变量组合 变量数量/个 归一化RMSE PCC
OV 2 0.168 0.788
AV 5 0.259 0.564
IV 2 0.109 0.821
OAV 7 0.264 0.569
OIV 4 0.086 0.843
AIV 7 0.178 0.766
OAIV 9 0.072 0.857
对OAIV变量组合进行随机超参数搜索,从而在无人为干涉的情况下寻找验证集损失最小的最优模型。批大小搜索范围为10~300,学习率搜索范围为10-3~10-5,全连接层激活函数搜索范围为selu、relu、sigmoid和tanh,LSTM层的神经元节点数搜索范围为100~250,数据的输入长度范围设置为1~384,间隔为25。搜索超参数组合设置为100组,每一组组合训练轮数为500轮,交叉验证折数设置为5。
随后利用Adam优化器最小化预测值和观测值之间的损失,设置学习率自动下降周期为50轮,如果在50轮中模型验证集预测值和观测值之间损失未下降,则将当前超参数组合中的学习率乘以系数0.2;同时设置在200轮中模型验证集预测值和观测值之间损失未下降则停止当前模型训练,以减少计算资源浪费。使用的损失函数是均方根误差,并将这一配置应用于其他模型。

3 结果与讨论

3.1 相对海平面变化趋势

1993—2020年6个验潮站的相对海平面实测记录均表现为上升趋势,各站平均的相对海平面变化速率为4.47±0.90 mm/a(表4),高于IPCC 2019年报告的1993—2018年由验潮仪和卫星测高数据估计的全球海平面变化速率3.2 mm/a[3]。在过去的研究中,CHEN等[44]利用在渤海、黄海、东海及南海选定的的10个验潮站数据,估计各个验潮站自有数据记录至2012年期间的相对海平面变化速率为1~5 mm/a;PARKER等[45]根据大埔滘、鲗鱼涌、大连、闸坡及坎门5个验潮站数据,估计各站自有数据记录至2016年期间的相对海平面变化速率为2.35~3.33 mm/a;ZHOU等[46]根据2003—2019年共17年的中国沿海验潮仪数据估计了这期间中国沿海相对海平面变化速率为5.46±1.10 mm/a。以上结果表明,在过去的半个世纪,中国沿海的相对海平面上升速率在不断加快。
表4 相对海平面变化趋势

Tab.4 Change trend of relative sea level

站点 站点代码 相对海平面变化速率/(mm·a-1)
大连 723 5.01±0.81
吕四 979 6.00±0.93
坎门 934 4.24±0.66
大埔滘 1034 3.30±0.82
闸坡 933 3.17±0.85
西沙 1745 5.10±1.35
平均值 4.47±0.90

3.2 绝对海平面变化趋势

根据1993—2020年6个验潮站所处区域的卫星测高数据得到的绝对海平面变化(表5)表明,所有6个站点及周围区域的绝对海平面均表现为上升趋势。各站平均的绝对海平面变化速率为4.17±1.32 mm/a,高于AVISO(Archiving,Validation and Interpretation of Satellite Oceanographic)数据中心根据Topex、Jason-1和Jason-2测高数据计算出的1993—2018年全球海平面上升速率3.3 mm/a[14]。
表5 绝对海平面变化趋势

Tab.5 Change trend of absolute sea level

站点 站点代码 绝对海平面变化速率/(mm·a-1)
大连 723 4.26±1.22
吕四 979 3.90±1.26
坎门 934 4.02±1.25
大埔滘 1034 3.97±1.87
闸坡 933 4.12±1.37
西沙 1745 4.76±0.96
平均值 4.17±1.32
以往的研究也发现了类似的绝对海平面上升趋势。QU等[47]利用AVISO卫星测高产品估计1993 — 2016年间渤海、黄海、东海及南海的18个验潮站周边海域的绝对海平面变化速率为(2.2±0.8)~(6.2±1.2)mm/a,平均变化速率为3.2±1.1 mm/a;FENG等[8]同样利用AVISO卫星测高产品估计1993—2016年间中国海平面上升速率在1~10 mm/a之间变化,平均上升速率为3.6±0.3 mm/a。对比上述结果可知,在过去的半个世纪,中国沿海的绝对海平面上升速率也在不断加快。

3.3 垂直地壳运动趋势

6个站点的垂直地壳运动趋势估计值(表6)表明:1993—2020年除大埔滘和闸坡验潮站外,其它4个验潮站所处区域的垂直地壳运动均表现为下沉趋势,其中吕四验潮站所在区域的沉降速率最快,为-2.25±1.17 mm/a。各站平均的垂直地壳运动变化速率为-0.52±1.05 mm/a。
表6 垂直地壳运动趋势

Tab.6 Change trend of vertical land movement

站点 站点代码 垂直地壳运动趋势/(mm·a-1)
大连 723 -1.01±0.95
吕四 979 -2.25±1.17
坎门 934 -0.48±1.33
大埔滘 1034 0.39±0.77
闸坡 933 0.68±0.76
西沙 1745 -0.42±1.29
平均值 -0.52±1.05

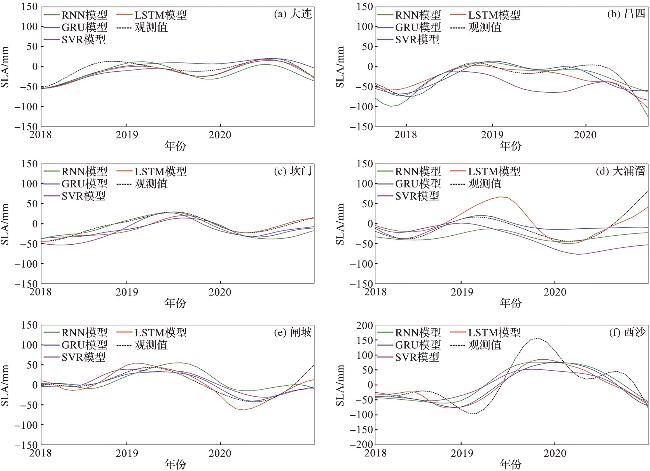
3.4 模型评估

将LSTM模型与RNN模型[48]、GRU模型[49]和SVR模型[50]等3种模型的预测性能进行比较,不同模型的结构和参数见表7。
表7 不同模型的结构和参数

Tab.7 Structures and parameters of different models

模型 模型结构
输入层 隐藏层 输出层
LSTM模型 (348,9) 150 1
RNN模型 (348,9) 150 1
GRU模型 (348,9) 150 1
SVR模型 Input Shape=(348,9);C=100;Gamma=0.001;Kernal:“Rbf”
在6个验潮站分别使用LSTM模型、GRU模型、RNN模型以及SVR模型预测2018—2020年的相对海平面变化(图3)。不同模型的归一化误差精度评估结果(表8)显示,LSTM模型在6个站点预测结果的RMSE均最小,PCC值均最大,说明LSTM模型预测效果最好。因此采用多变量LSTM模型对6个验潮站未来3年(2021—2023年)的相对海平面变化进行预测和对比分析。
图3 不同模型的预测结果对比

Fig.3 Comparison of prediction results of different models

表8 不同模型预测结果的归一化精度评估

Tab.8 Normalized accuracy evaluation of prediction results of different models

站点 指标 RNN模型 GRU模型 SVR模型 LSTM模型
大连 PCC 0.849 0.880 0.756 0.911
RMSE 0.146 0.132 0.164 0.115
吕四 PCC 0.807 0.809 0.619 0.828
RMSE 0.061 0.059 0.098 0.047
坎门 PCC 0.829 0.846 0.813 0.877
RMSE 0.086 0.082 0.094 0.071
大埔滘 PCC 0.488 0.665 0.259 0.728
RMSE 0.181 0.156 0.246 0.146
闸坡 PCC 0.651 0.864 0.788 0.941
RMSE 0.095 0.079 0.097 0.071
西沙 PCC 0.822 0.856 0.799 0.908
RMSE 0.133 0.131 0.154 0.112

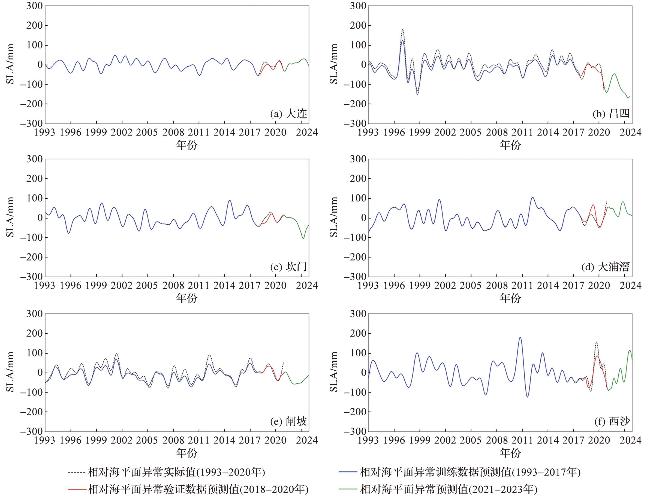
3.5 最优模型预测结果

将6个验潮站1993—2017年间的数据作为模型训练集,2018—2020年间的数据作为模型验证集,使用OAIV变量组合的LSTM模型对6个验潮站的相对海平面变化进行预测,并对预测结果进行评估(表9)。评估结果显示,除大埔滘站外其余所有站点预测结果的PCC均大于0.820,各站点平均的PCC值为0.866,RSME为19.279 mm,说明以海洋、大气及气候模态指数变量作为预报因子组合能够帮助LSTM模型较好地预测这些站点所在区域的海平面变化。
表9 LSTM模型预测性能评估

Tab.9 Prediction performance evaluation of LSTM model

站点 RMSE/mm PCC
大连 11.841 0.911
吕四 18.836 0.828
坎门 12.014 0.877
大埔滘 26.438 0.728
闸坡 12.416 0.941
西沙 34.132 0.908
平均值 19.279 0.866
6个验潮站相对海平面变化的LSTM模型预测结果如图4所示,图中黑色曲线代表从各个站点验潮仪数据中分离出的相对海平面异常值(1993—2020年),蓝色曲线代表本文使用的LSTM模型训练集预测结果(1993—2017年),红色曲线代表本文使用的LSTM模型验证集预测结果(2018—2020年),绿色曲线代表LSTM模型对未来3年(2021—2023年)的相对海平面异常预测结果,即模型测试集预测结果。从各站点的预测结果和实测值的对比可以看出,虽然在极大值和极小值处存在差异,但预测值与实测值的变化趋势一致,能够准确把握相对海平面年际变化的特征。
图4 LSTM模型在各验潮站的预测结果

Fig.4 Prediction results of LSTM model at each tidal gauge station

4 结论

本文利用大气、海洋及气候模态指数变量作为预报因子,建立多种神经网络模型对中国沿海6个验潮站的相对海平面变化趋势进行了回归分析,得到如下结论。
1)同时输入海洋、大气和气候模态指数变量作为预报因子的模型,预测性能要优于采用其他预报因子组合的模型。添加PDO指数和Niño3.4指数后预测结果误差更小、拟合效果更好,能够准确把握海平面年际变化的特征,可以考虑将气候模态作为探究利用机器学习预测海平面异常的一种新参考。
2)经过与GRU模型、RNN模型以及SVR模型的对比可知,在相同配置和输入数据的情况下,LSTM模型的预测性能优于其他3种模型。
3)基于多变量LSTM人工神经网络模型构建的海平面预测模型经过交叉验证后的各站点平均的PCC值为0.866,RSME为19.279 mm,预测结果较为理想,可以作为一种新型的海平面预测手段。
4)中国沿海的平均相对海平面上升速率和绝对海平面上升速率均超出全球平均水平,上升速率在不断加快。中国沿海的平均相对海平面上升速率大于绝对海平面上升速率,表明中国沿海存在总体上为负的垂直地壳运动趋势。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
MASSON-DELMOTTE V, ZHAI P, PIRANI A, et al. Climate change 2021: The physical science basis[M]. Cambridge, UK and New York, NY, USA: Cambridge University Press, 2021: 2391.

[2]
VERMEER M, RAHMSTORF S. Global sea level linked to global temperature[J]. Proceedings of the National Academy of Sciences of the United States of America, 2009, 106(51): 21527-21532.

DOI PMID

[3]
OPPENHEIMER M, GLAVOVIC B, HINKEL J, et al. Sea level rise and implications for low-lying islands, coasts and communities[M]//IPCC special report on the ocean and cryosphere in a changing climate. Cambridge, UK and New York, NY, USA: Cambridge University Press, 2019: 321-445.

[4]
NEREM R S, BECKLEY B D, FASULLO J T, et al. Climate-change-driven accelerated sea-level rise detected in the altimeter era[J]. Proceedings of the National Academy of Sciences of the United States of America, 2018, 115(9): 2022-2025.

DOI PMID

[5]
自然资源部. 2022年中国海平面公报[EB/OL].(2023-04-05)[2023-08-25]. http://gi.mnr.gov.cn/202304/t20230412_2781114.html.

[6]
WOODWORTH P L, MELET A, MARCOS M, et al. Forcing factors affecting sea level changes at the coast[J]. Surveys in Geophysics, 2019, 40(6): 1351-1397.

DOI

[7]
WANG Q S, PAN C H, ZHANG G Z. Impact of and adaptation strategies for sea-level rise on Yangtze River Delta[J]. Advances in Climate Change Research, 2018, 9(2): 154-160.

[8]
FENG X B, CHENG Y C. Observing sea levels in the China Seas from satellite altimetry[M]//Remote sensing of the Asian seas. Cham: Springer International Publishing, 2018: 321-338.

[9]
MENG L S, ZHUANG W, ZHANG W W, et al. Decadal sea level variability in the Pacific Ocean: Origins and climate mode contributions[J]. Journal of Atmospheric and Oceanic Technology, 2019, 36(4): 689-698.

[10]
XI H, ZHANG Z Z, LU Y, et al. Long-term and interannual variation of the steric sea level in the South China Sea and the connection with ENSO[J]. Journal of Coastal Research, 2019, 35(3): 489.

[11]
SITHARA S, PRAMADA S K, THAMPI S G. Sea level prediction using climatic variables: A comparative study of SVM and hybrid wavelet SVM approaches[J]. Acta Geophysica, 2020, 68(6): 1779-1790.

[12]
ZUBIER K M, EYOUNI L S. Investigating the role of atmospheric variables on sea level variations in the eastern central Red Sea using an artificial neural network approach[J]. Oceanologia, 2020, 62(3): 267-290.

[13]
BALOGUN A L, ADEBISI N. Sea level prediction using ARIMA, SVR and LSTM neural network: Assessing the impact of ensemble ocean-atmospheric processes on models’ accuracy[J]. Geomatics, Natural Hazards and Risk, 2021, 12(1): 653-674.

[14]
ADEBISI N, BALOGUN A L. A deep-learning model for national scale modelling and mapping of sea level rise in Malaysia: The past, present, and future[J]. Geocarto International, 2022, 37(23): 6892-6914.

[15]
MUSLIM T O, AHMED A N, MALEK M A, et al. Investigating the influence of meteorological parameters on the accuracy of sea-level prediction models in Sabah, Malaysia[J]. Sustainability, 2020, 12(3): 1193.

[16]
FU Y G, ZHOU X H, SUN W K, et al. Hybrid model combining empirical mode decomposition, singular spectrum analysis, and least squares for satellite-derived sea-level anomaly prediction[J]. International Journal of Remote Sensing, 2019, 40(20): 7817-7829.

[17]
ISLAM B U, AHMED S F. Short-term electrical load demand forecasting based on LSTM and RNN deep neural networks[J]. Mathematical Problems in Engineering, 2022, 2022: 2316474.

[18]
MAKRIDAKIS S, SPILIOTIS E, ASSIMAKOPOULOS V. Statistical and machine learning forecasting methods: Concerns and ways forward[J]. PLoS One, 2018, 13(3): e0194889.

[19]
FARINOTTI D, HUSS M, FÜRST J J, et al. A consensus estimate for the ice thickness distribution of all glaciers on earth[J]. Nature Geoscience, 2019, 12: 168-173.

[20]
SAENKO O A, YANG D, GREGORY J M, et al. Separating the influence of projected changes in air temperature and wind on patterns of sea level change and ocean heat content[J]. Journal of Geophysical Research: Oceans, 2015, 120(8): 5749-5765.

[21]
SMITH-KONTER B R, THORNTON G M, SANDWELL D T. Vertical crustal displacement due to interseismic deformation along the San Andreas fault: Constraints from tide gauges[J]. Geophysical Research Letters, 2014, 41(11): 3793-3801.

[22]
SUZUKI T, ISHII M. Long-term regional sea level changes due to variations in water mass density during the period 1981-2007[J]. Geophysical Research Letters, 2011, 38(21): L21604.

[23]
OSTANCIAUX É, HUSSON L, CHOBLET G, et al. Present-day trends of vertical ground motion along the coast lines[J]. Earth-Science Reviews, 2012, 110(1/2/3/4): 74-92.

[24]
PFEFFER J, SPADA G, MÉMIN A, et al. Decoding the origins of vertical land motions observed today at coasts[J]. Geophysical Journal International, 2017, 210(1): 148-165.

[25]
RAUCOULES D, LE COZANNET G, WÖPPELMANN G, et al. High nonlinear urban ground motion in Manila (Philippines) from 1993 to 2010 observed by DInSAR: Implications for sea-level measurement[J]. Remote Sensing of Environment, 2013, 139: 386-397.

[26]
HELIANI L S, WIDJAJANTI N, ENDRAYANTO I, et al. Preprocessing of coastal satellite altimetry, tide gauges, and GNSS data: Towards the possibility of detected vertical deformation of south Java Island[J]. Procedia Environ-mental Sciences, 2013, 17: 308-316.

[27]
ROVERE A, RAYMO M E, VACCHI M, et al. The analysis of last interglacial (MIS 5e) relative sea-level indicators: Reconstructing sea-level in a warmer world[J]. Earth-Science Reviews, 2016, 159: 404-427.

[28]
VIGNUDELLI S, BIROL F, BENVENISTE J, et al. Satellite altimetry measurements of sea level in the coastal zone[J]. Surveys in Geophysics, 2019, 40(6): 1319-1349.

DOI

[29]
TANG X H, WANG F, CHEN Y L, et al. Warming trend in northern East China Sea in recent four decades[J]. Chinese Journal of Oceanology and Limnology, 2009, 27(2): 185-191.

[30]
CHEN Z Y, WANG Z H. Yangtze Delta, China: Taihu lake-level variation since the 1950s, response to sea-level rise and human impact[J]. Environmental Geology, 1999, 37(4): 333-339.

[31]
WU P, VAN DER WAL W. Postglacial sealevels on a spherical, self-gravitating viscoelastic earth: Effects of lateral viscosity variations in the upper mantle on the inference of viscosity contrasts in the lower mantle[J]. Earth and Planetary Science Letters, 2003, 211(1/2): 57-68.

[32]
YIN J, YU D P, YIN Z E, et al. Modelling the combined impacts of sea-level rise and land subsidence on storm tides induced flooding of the Huangpu River in Shanghai, China[J]. Climatic Change, 2013, 119(3): 919-932.

[33]
ZOU F, TENZER R, FOK H S, et al. The sea-level changes in Hong Kong from tide-gauge records and remote sensing observations over the last seven decades[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 6777-6791.

[34]
郭金运, 王建波, 胡志博, 等. 由TOPEX/Poseidon和Jason-1/2探测的1993—2012中国海海平面时空变化[J]. 地球物理学报, 2015, 58(9):3103-3120.

DOI

GUO J Y, WANG J B, HU Z B, et al. Temporal-spatial variations of sea level over China seas derived from altimeter data of TOPEX/Poseidon, Jason-1 and Jason-2 from 1993 to 2012[J]. Chinese Journal of Geophysics, 2015, 58(9): 3103-3120.

[35]
李建成, 王正涛, 胡建国. 联合多种卫星测高数据分析全球和中国海海平面变化[J]. 武汉测绘科技大学学报, 2000, 25(4):343-347.

LI J C, WANG Z T, HU J G. Mean sea level variation using historic satellite altimeter data[J]. Geomatics and Information Science of Wuhan University, 2000, 25(4): 343-347.

[36]
CHENG X H, QI Y Q. Trends of sea level variations in the South China Sea from merged altimetry data[J]. Global and Planetary Change, 2007, 57(3/4): 371-382.

[37]
詹金刚, 王勇, 柳林涛. 中国近海海平面季节尺度变化的时频分析[J]. 地球物理学报, 2003, 46(1):36-41.

ZHAN J G, WANG Y, LIU L T. Time-frequency analysis of the inter-seasonal variations of China-neighboring seas level[J]. Chinese Journal of Geophysics, 2003, 46(1): 36-41.

[38]
AL-JABERY K, OBAFEMI-AJAYI T, OLBRICHT G, et al. Computational learning approaches to data analytics in biomedical applications[M]. London: Academic Press, 2020.

[39]
ISHIDA K, TSUJIMOTO G, ERCAN A L, et al. Hourly-scale coastal sea level modeling in a changing climate using long short-term memory neural network[J]. Science of the Total Environment, 2020, 720: 137613.

[40]
BERGSTRA J, BENGIO Y. Random search for hyper-parameter optimization[J]. Journal of Machine Learning Research, 2012, 13: 281-305.

[41]
WÖPPELMANN G, MARCOS M. Vertical land motion as a key to understanding sea level change and variability[J]. Reviews of Geophysics, 2016, 54(1): 64-92.

[42]
于振龙, 许东峰, 姚志雄, 等. 基于多变量LSTM神经网络模型的PDO指数预测研究[J]. 海洋学报, 2022, 44(6):58-67.

YU Z L, XU D F, YAO Z X, et al. Research on PDO index prediction based on multivariate LSTM neural network model[J]. Haiyang Xuebao, 2022, 44(6): 58-67.

[43]
HYNDMAN R J, KOEHLER A B. Another look at measures of forecast accuracy[J]. International Journal of Forecasting, 2006, 22(4): 679-688.

[44]
CHEN N, HAN G Q, YANG J S. Mean relative sea level rise along the coasts of the China Seas from mid-20th to 21st centuries[J]. Continental Shelf Research, 2018, 152: 27-34.

[45]
PARKER A. Relative sea level rise along the coast of China mid-twentieth to end twenty-first centuries[J]. Arabian Journal of Geosciences, 2018, 11: 262.

[46]
ZHOU D X, LIU Y, FENG Y K, et al. Absolute sea level changes along the coast of China from tide gauges, GNSS, and satellite altimetry[J]. Journal of Geophysical Research: Oceans, 2022, 127(9): e2022JC018994.

[47]
QU Y, JEVREJEVA S, JACKSON L P, et al. Coastal sea level rise around the China Seas[J]. Global and Planetary Change, 2019, 172: 454-463.

DOI

[48]
CONNOR J T, MARTIN R D, ATLAS L E. Recurrent neural networks and robust time series prediction[J]. IEEE Transactions on Neural Networks, 1994, 5(2): 240-254.

DOI PMID

[49]
CHUNG J, GULCEHRE C, CHO K H, et al. Empirical evaluation of gated recurrent neural networks on sequence modeling[Z/OL]. arXiv, 2023: 1412.3555. https://arxiv.org/abs/1412.3555.

[50]
CORTES C, VAPNIK V. Support-vector networks[J]. Machine Learning, 1995, 20(3): 273-297.

Options
Outlines

/

〈 〉