0 引言
1 涌潮的数值模拟
1.1 数值模型方法
1.1.1 控制方程
1.1.2 湍流模型
1.1.3 自由边界条件
1.1.4 离散方法
1.2 数值验证
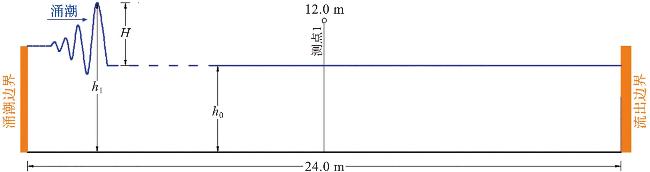
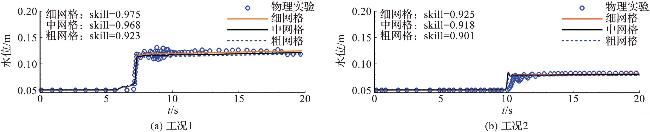
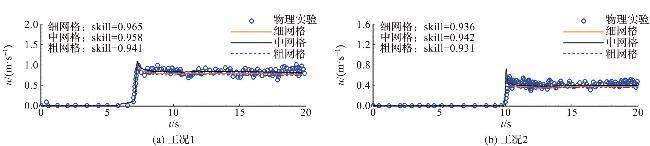
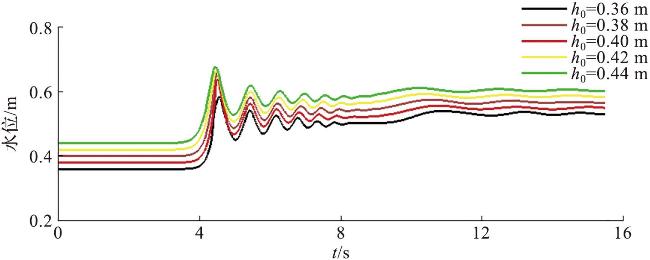
图2 物理实验验证工况下x=10 m处的水位时程曲线Fig.2 Temporal evolution of water level in verification of physical experimental conditions at x=10 m |
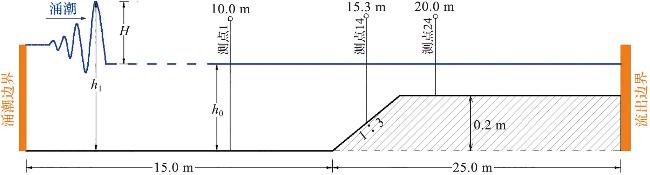
1.3 波状涌潮在斜坡地形上传播演变的数值模拟
表2 数值模拟工况Tab.2 Numerical simulation conditions |
| 工况序号 | 潮前水深 h0/m | 波高H/m | 潮后水深 h1/m | 潮后流速 u1/(m·s-1) | Fr | 工况序号 | 潮前水深 h0/m | 波高H/m | 潮后水深 h1/m | 潮后流速 u1/(m·s-1) | Fr |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.36 | 0.14 | 0.50 | 0.678 | 1.288 | 14 | 0.42 | 0.16 | 0.58 | 0.718 | 1.282 |
| 2 | 0.38 | 0.14 | 0.52 | 0.662 | 1.273 | 15 | 0.44 | 0.16 | 0.60 | 0.703 | 1.269 |
| 3 | 0.40 | 0.14 | 0.54 | 0.647 | 1.259 | 16 | 0.37 | 0.12 | 0.49 | 0.579 | 1.241 |
| 4 | 0.42 | 0.14 | 0.56 | 0.633 | 1.247 | 17 | 0.38 | 0.12 | 0.50 | 0.572 | 1.234 |
| 5 | 0.44 | 0.14 | 0.58 | 0.620 | 1.236 | 18 | 0.40 | 0.13 | 0.53 | 0.603 | 1.241 |
| 6 | 0.37 | 0.15 | 0.52 | 0.715 | 1.300 | 19 | 0.42 | 0.13 | 0.55 | 0.590 | 1.230 |
| 7 | 0.38 | 0.15 | 0.53 | 0.706 | 1.292 | 20 | 0.44 | 0.13 | 0.57 | 0.578 | 1.219 |
| 8 | 0.40 | 0.15 | 0.55 | 0.690 | 1.278 | 21 | 0.37 | 0.11 | 0.48 | 0.533 | 1.221 |
| 9 | 0.42 | 0.15 | 0.57 | 0.676 | 1.265 | 22 | 0.38 | 0.11 | 0.49 | 0.527 | 1.215 |
| 10 | 0.44 | 0.15 | 0.59 | 0.662 | 1.253 | 23 | 0.40 | 0.12 | 0.52 | 0.559 | 1.223 |
| 11 | 0.37 | 0.13 | 0.50 | 0.624 | 1.260 | 24 | 0.42 | 0.12 | 0.54 | 0.547 | 1.212 |
| 12 | 0.38 | 0.13 | 0.51 | 0.617 | 1.254 | 25 | 0.44 | 0.12 | 0.56 | 0.535 | 1.203 |
| 13 | 0.40 | 0.16 | 0.56 | 0.734 | 1.296 |
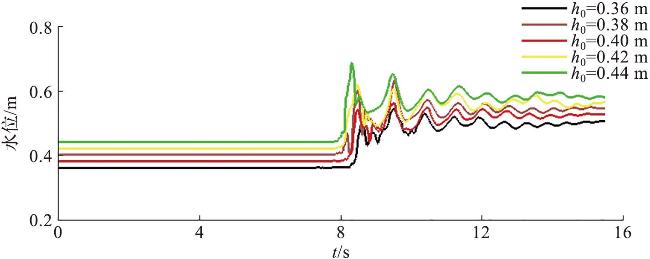
图5 在1~5号数值模拟工况下x=10 m处的水位时程曲线Fig.5 Temporal evolution of water level in numerical simulation conditions 1-5 at x=10 m |
2 卷积神经网络在涌潮预测中的应用
2.1 数据集
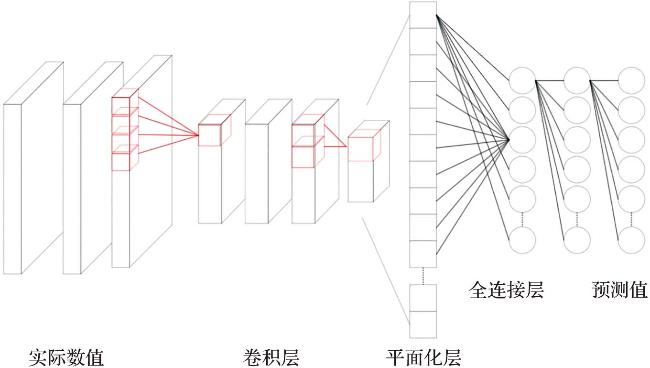
2.2 网络配置
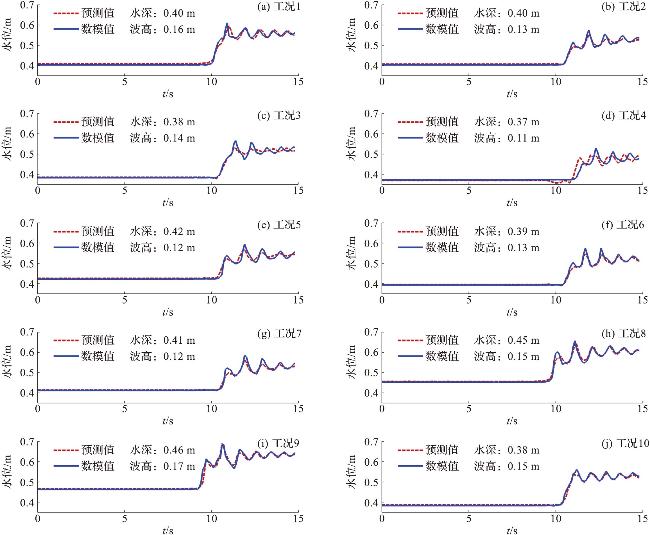
2.3 训练结果
表3 测试工况设置Tab.3 Test conditions |
| 工况序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 水深/m | 0.40 | 0.40 | 0.38 | 0.37 | 0.42 | 0.39 | 0.41 | 0.45 | 0.46 | 0.38 |
| 波高/m | 0.16 | 0.13 | 0.14 | 0.11 | 0.12 | 0.13 | 0.12 | 0.15 | 0.17 | 0.15 |
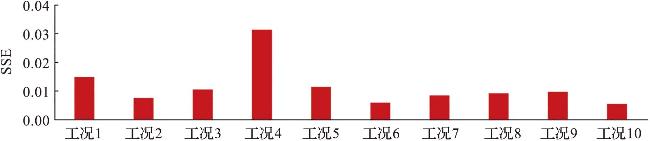
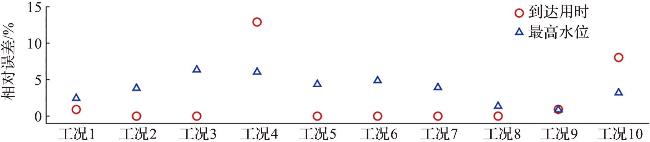
表4 不同测试工况下涌潮到达 x=30.0 m 测点处的用时和该测点最高水位的CONV1D模型预测值与数值模拟值的误差分析Tab.4 Error analysis between CONV1D model predicted and numerical simulations of the time taken for the tidal bore reaching and maximum water level at x=30.0 m under different test conditions |
| 工况序号 | 涌潮到达 x=30.0 m 测点处的用时 | x=30.0 m 测点处的最高水位 | ||||
|---|---|---|---|---|---|---|
| 数值模拟值/s | CONV1D模型预测值/s | 相对误差/% | 数值模拟值/m | CONV1D模型预测值/m | 相对误差/% | |
| 1 | 11.0 | 11.1 | 0.91 | 0.611 | 0.596 | 2.45 |
| 2 | 12.0 | 12.0 | 0.00 | 0.575 | 0.553 | 3.83 |
| 3 | 11.5 | 11.5 | 0.00 | 0.567 | 0.531 | 6.35 |
| 4 | 12.4 | 14.0 | 12.90 | 0.530 | 0.498 | 6.04 |
| 5 | 12.0 | 12.0 | 0.00 | 0.595 | 0.569 | 4.37 |
| 6 | 11.7 | 11.7 | 0.00 | 0.575 | 0.547 | 4.87 |
| 7 | 12.0 | 12.0 | 0.00 | 0.585 | 0.562 | 3.93 |
| 8 | 11.2 | 11.2 | 0.00 | 0.658 | 0.649 | 1.37 |
| 9 | 10.8 | 10.7 | 0.93 | 0.684 | 0.690 | 0.88 |
| 10 | 11.2 | 12.1 | 8.04 | 0.562 | 0.544 | 3.20 |