0 引言
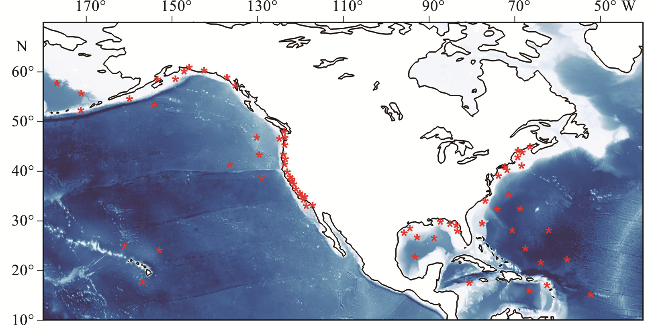
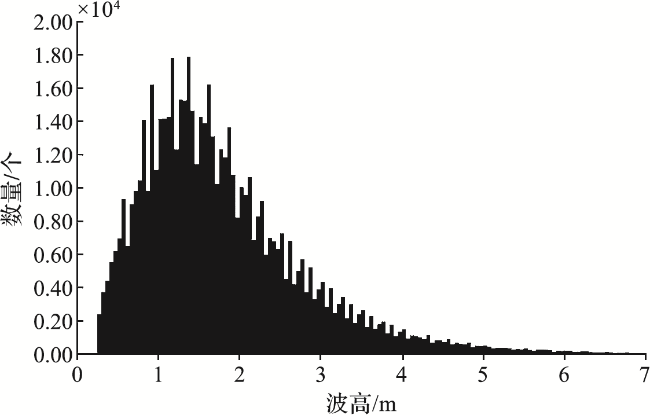
1 数据
表1 70个NDBC浮标站点信息Tab.1 Information of 70 NDBC buoy stations |
| 序号 | NDBC站点序号 | 经度 | 纬度 | 站点水深/m | 序号 | NDBC站点序号 | 经度 | 纬度 | 站点水深/m |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 41001 | 72.242°W | 34.703°N | 4 501.0 | 36 | 46012 | 122.881°W | 37.356°N | 208.8 |
| 2 | 41002 | 74.936°W | 31.759°N | 3 784.0 | 37 | 46013 | 123.317°W | 38.235°N | 127.0 |
| 3 | 41010 | 78.485°W | 28.878°N | 890.0 | 38 | 46014 | 123.974°W | 39.231°N | 356.0 |
| 4 | 41013 | 77.764°W | 33.441°N | 33.0 | 39 | 46015 | 124.844°W | 42.752°N | 446.0 |
| 5 | 41040 | 53.130°W | 14.532°N | 4 944.0 | 40 | 46022 | 124.527°W | 40.748°N | 419.0 |
| 6 | 41043 | 64.793°W | 21.026°N | 5 262.0 | 41 | 46026 | 122.839°W | 37.754°N | 54.9 |
| 7 | 41044 | 58.630°W | 21.582°N | 5 419.0 | 42 | 46027 | 124.382°W | 41.840°N | 60.0 |
| 8 | 41046 | 68.393°W | 23.822°N | 5 490.0 | 43 | 46028 | 121.903°W | 35.770°N | 1 154.0 |
| 9 | 41047 | 71.452°W | 27.465°N | 5 347.0 | 44 | 46029 | 124.487°W | 46.163°N | 131.0 |
| 10 | 41048 | 69.573°W | 31.831°N | 5 394.0 | 45 | 46035 | 177.703°W | 57.016°N | 3 694.0 |
| 11 | 41049 | 62.938°W | 27.490°N | 5 459.0 | 46 | 46041 | 124.739°W | 47.352°N | 131.0 |
| 12 | 42001 | 89.662°W | 25.926°N | 3 200.0 | 47 | 46042 | 122.396°W | 36.785°N | 1 693.0 |
| 13 | 42002 | 93.646°W | 26.055°N | 3 088.0 | 48 | 46047 | 119.525°W | 32.388°N | 1 423.0 |
| 14 | 42019 | 95.345°W | 27.910°N | 83.5 | 49 | 46050 | 124.546°W | 44.669°N | 160.0 |
| 15 | 42020 | 96.687°W | 26.955°N | 84.0 | 50 | 46053 | 119.839°W | 34.241°N | 405.0 |
| 16 | 42036 | 84.508°W | 28.501°N | 50.9 | 51 | 46054 | 120.468°W | 34.274°N | 454.0 |
| 17 | 42039 | 86.000°W | 28.787°N | 281.0 | 52 | 46059 | 129.976°W | 38.069°N | 4 640.0 |
| 18 | 42040 | 88.237°W | 29.207°N | 192.0 | 53 | 46061 | 146.833°W | 60.283°N | 222.0 |
| 19 | 42055 | 94.112°W | 22.140°N | 3 608.0 | 54 | 46066 | 155.009°W | 52.765°N | 4 457.0 |
| 20 | 42057 | 81.462°W | 16.918°N | 368.0 | 55 | 46069 | 120.213°W | 33.677°N | 977.8 |
| 21 | 42059 | 67.483°W | 15.300°N | 4 761.0 | 56 | 46071 | 180.216°W | 51.022°N | 4 018.0 |
| 22 | 42099 | 84.275°W | 27.349°N | 93.9 | 57 | 46072 | 172.114°W | 51.666°N | 3 566.0 |
| 23 | 44005 | 69.127°W | 43.201°N | 176.8 | 58 | 46073 | 172.012°W | 55.008°N | 3 471.0 |
| 24 | 44007 | 70.140°W | 43.525°N | 49.0 | 59 | 46075 | 160.794°W | 53.969°N | 2 318.0 |
| 25 | 44008 | 69.250°W | 40.496°N | 72.0 | 60 | 46076 | 148.009°W | 59.471°N | 192.0 |
| 26 | 44009 | 74.692°W | 38.460°N | 24.0 | 61 | 46077 | 154.211°W | 57.869°N | 200.0 |
| 27 | 44013 | 70.651°W | 42.346°N | 64.6 | 62 | 46080 | 150.042°W | 57.947°N | 254.5 |
| 28 | 44018 | 70.154°W | 42.203°N | 43.9 | 63 | 46082 | 143.353°W | 59.670°N | 296.0 |
| 29 | 44025 | 73.164°W | 40.251°N | 36.3 | 64 | 46083 | 138.019°W | 58.270°N | 128.9 |
| 30 | 44027 | 67.300°W | 44.283°N | 191.4 | 65 | 46084 | 136.102°W | 56.622°N | 1 158.0 |
| 31 | 44066 | 72.644°W | 39.618°N | 77.0 | 66 | 46086 | 118.052°W | 32.499°N | 1 844.7 |
| 32 | 46002 | 130.507°W | 42.662°N | 3 478.0 | 67 | 46089 | 125.793°W | 45.936°N | 2 375.0 |
| 33 | 46005 | 131.079°W | 46.134°N | 2 852.0 | 68 | 51000 | 153.792°W | 23.528°N | 4 762.0 |
| 34 | 46006 | 137.377°W | 40.764°N | 4 347.0 | 69 | 51002 | 157.746°W | 17.042°N | 4 997.0 |
| 35 | 46011 | 120.998°W | 34.936°N | 419.0 | 70 | 51101 | 162.081°W | 24.359°N | 4 860.0 |
2 方法
2.1 JONSWAP谱估算方法
2.2 三阶Stokes波的非线性海浪谱估算方法
2.3 海浪谱评估方法
3 结果
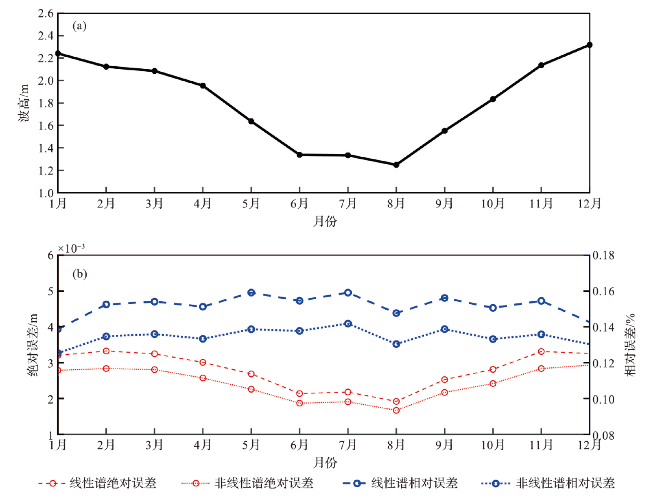
3.1 总体评估结果
表2 线性谱和非线性谱反演波高与实测波高的平均偏差和均方根误差Tab.2 Mean bias and root mean square error between inverted wave heights from linear and nonlinear spectra and measured wave heights |
| 海浪谱 | 平均偏差/m | 平均均方根误差/m |
|---|---|---|
| 线性谱 | -0.002 2 | 0.003 7 |
| 非线性谱 | -0.001 1 | 0.003 1 |
表3 非线性谱相较于线性谱反演结果提升程度统计Tab.3 Statistics on the improvement degree of inversion results from nonlinear spectrum relative to linear spectrum |
| 误差指标 | 最大提升程度/% | 最小提升程度/% | 平均提升程度/% | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 全部 波高 | 波高 >3 m | 全部 波高 | 波高 >3 m | 全部 波高 | 波高 >3 m | ||||
| 相对误差 | 22.29 | 47.73 | 1.68 | 4.69 | 11.19 | 24.07 | |||
| 绝对误差 | 28.54 | 49.58 | 2.28 | 4.18 | 13.05 | 24.74 | |||
| 包络面积 | 98.59 | 18.10 | 55.16 | ||||||
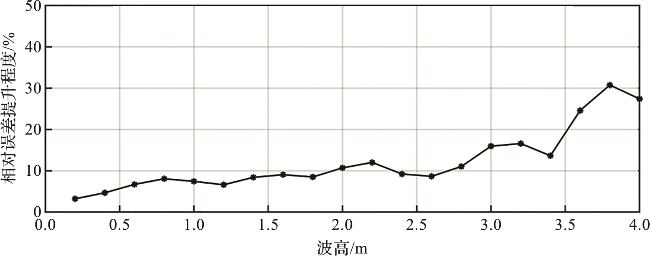
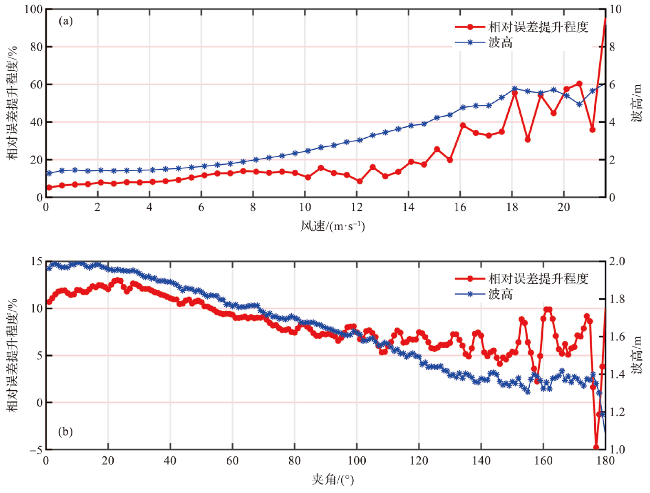
3.2 反演结果提升程度与波高的关系
3.3 反演结果提升程度与风速、风向与波向夹角的关系
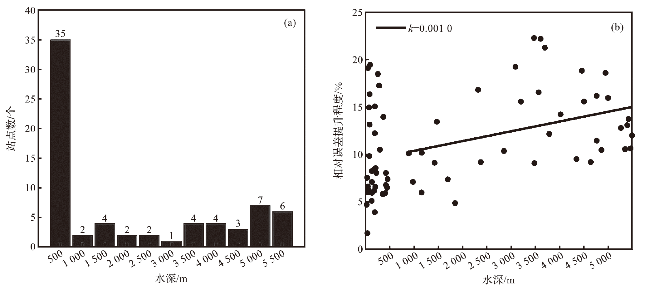
3.4 反演结果提升程度与浮标站点水深的关系
表4 在不同水深区间线性谱与非线性谱反演结果比较Tab.4 Comparison of results between linear and nonlinear spectrum inversion results for different water depth intervals |
| 水深/m | 相对误差/m | 非线性谱相对误差 提升程度/% | 偏差/m | 标准差/m | 均方根误差/m | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 线性谱 | 非线性谱 | 线性谱 | 非线性谱 | 线性谱 | 非线性谱 | 线性谱 | 非线性谱 | ||||
| 0~500 | 0.146 9 | 0.133 3 | 9.26 | -0.002 0 | -0.000 8 | 0.002 5 | 0.002 7 | 0.003 2 | 0.002 9 | ||
| 500~5 500 | 0.155 5 | 0.136 4 | 12.28 | -0.002 7 | -0.001 4 | 0.003 0 | 0.003 1 | 0.004 1 | 0.003 4 | ||