0 引言
1 双声道波导声传播模型
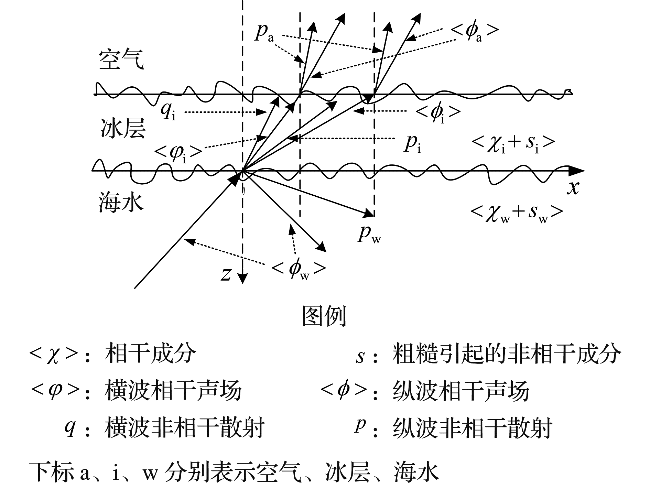
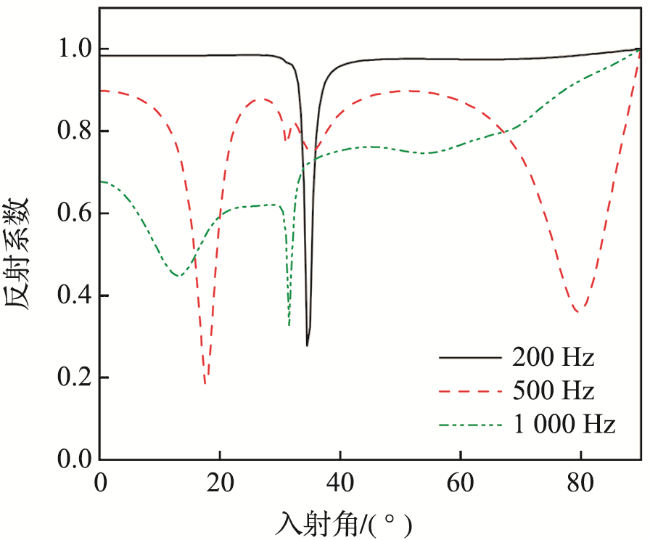
1.1 空气-冰层-海水反射特性
1.2 射线理论模型
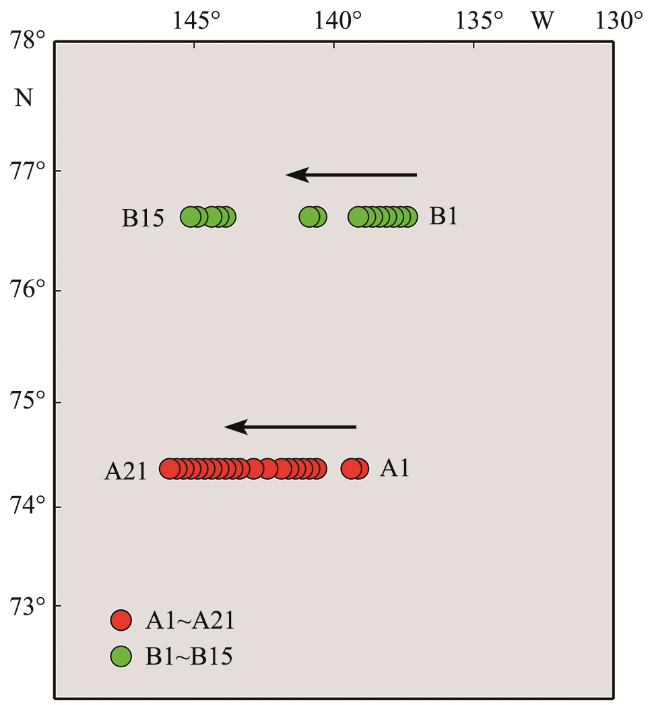
1.3 数据与方法
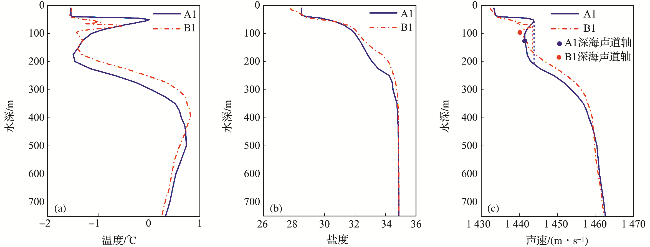
图4 A1点和B1点的温度、盐度和声速剖面(图c中的蓝色虚线、橙色虚线分别为声速剖面A1、声速剖面B1的深海声道上、下边界的连线。) Fig.4 Profile of temperature, salinity and speed of sound at point A1 and B1 (The blue dashed line and the orange dashed line in figure C are the lines connecting the upper and lower boundaries of the deep-sea acoustic channel for sound velocity profile A1 and sound velocity profile B1 respectively.) |
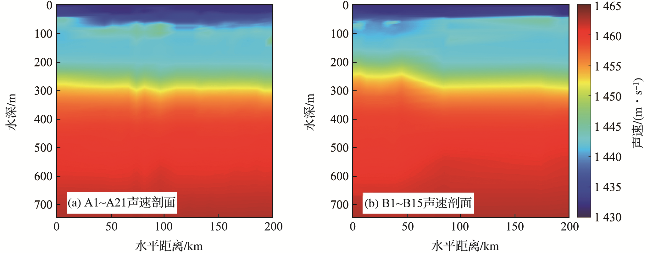
图5 A1-A21、 B1-B15声速剖面(A1-A21、B1-B15实际距离分别为202 km、199.2 km,为便于展示,在图中均显示为200 km。) Fig.5 Sound velocity profiles of A1-A21, B1-B15 (The actual distances of A1-A21 and B1-B15 are 202 km and 199.2 km, respectively, which are shown as 200 km in this figure for the convenience of presentation.) |