0 引言
数字高程模型(digital elevation model,DEM)是一种重要的地理数据模型,在表达地貌形态、认知地表与研究地质构造等领域发挥着基础性作用[1-2]。而海底数字高程模型精度的高低将直接影响到海洋空间信息的准确性。近年来,随着多波束测深技术的发展,大量研究以多波束测深数据为源数据,通过各种插值方法构建数字高程模型,在插值方法、插值精度、数据质量评估方面已经有很多成果[3]。然而单波束测深仪由于其成本低、便于携带、数据处理简单等优点是探测近海海底地形地貌的主要方法之一[4],尤其是在近海、潮间带以及河道湖泊等区域仍然被广泛应用。目前已有大量针对稀疏的离散重力点、高程异常点的内插方法的研究[5-6],而利用稀疏单波束测深数据构建数字高程模型的研究较少。因此本文利用单波束测深数据,使用4种空间插值方法构建潮间带数字高程模型并分析模型的精度。
在陆地可以采用格网点的高程精度来衡量陆地地表地貌数字高程模型的精度[7],同理,在潮间带也可以利用潮间带地形点的高程精度来衡量潮间带地形数字高程模型的精度。然而获取潮间带地形点的高程精度较为困难,由此导致潮间带数字高程模型的精度验证困难。目前无人机摄影测量技术凭借其灵活度高、测量成本低以及效率高等优点已经被广泛应用于地形测量、海岸线测量以及海岸线变化监测等领域[8⇓-10],测量精度可达到厘米级[11]。并且无人机后处理差分(post-processing kinematic,PPK)技术的应用使得摄影测量能够获取高精度潮间带数字表面模型(digital surface model,DSM),DSM不仅包含了地形的高程信息,还涵盖了地面以外的其他地表信息的高程。
潮间带是大潮期最高潮位和最低潮位间的海岸[12],其交替性淹没或出露海水[13]。因而无人机航测能够在低潮时获取精度较高的潮间带数字高程数据。本研究通过无人机摄影测量结合单波束测深的方法不仅提高了潮间带数字高程数据的可靠性,并且利用潮间带的特殊地形,提出了一种以无人机PPK技术作为评价标准的单波束测深数据插值精度分析方法,能够解决在潮间带区域使用单波束数据进行插值时精度验证困难的问题,也可为海水较深区域使用插值模型提供可靠的选取依据。与传统交叉线检查方法相比,本文中的方法在评估精度时能够验证面积更广的区域,并且无人机航测相对于船载测量成本更低、效率更高。具体操作步骤为在高潮时使用单波束测深仪结合全球导航卫星系统(global navigation satellite system,GNSS)获取带有三维坐标的水下地形点作为插值分析源数据;使用克里金插值法、反距离权重法、样条函数法以及自然邻域法4种插值方法进行插值,构建潮间带数字高程模型;在低潮时基于无人机摄影测量构建高精度的潮间带数字表面模型作为潮间带数字高程模型的精度评价标准,对4种插值方法所构建的潮间带数字高程模型进行精度分析。
1 材料与方法
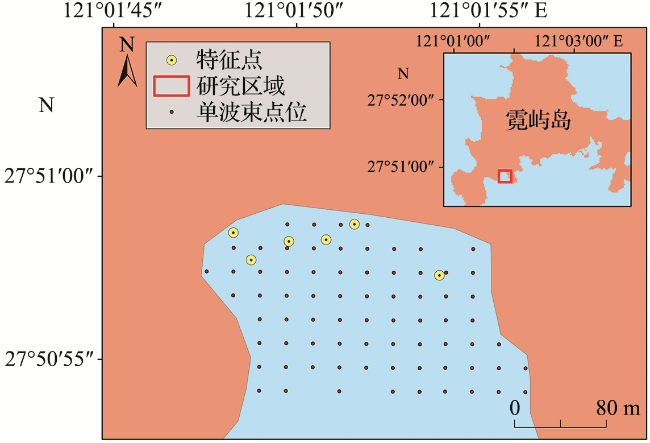
1.1 研究区域概况
以浙江省温州市洞头区霓屿岛某潮间带为研究区域。霓屿岛面积约10.43 km2,岸线长30.18 km,周围有面积约14.28 km2的大片滩涂。研究区域水深范围为0~2 m,潮间带为泥质滩涂,潮上带被砾石填充,适合在其中布设特征点用以进行精度评估(图1)。
1.2 数据来源
表1 单波束测深仪参数Tab.1 Single-beam sounder parameters |
| 规格型号 | 项目 | 技术指标 |
|---|---|---|
| HY1601单频测深仪 | 工作频率 | 208 kHz |
| 分辨率 | 0.01 m | |
| 最大水深 | 0.3~300 m | |
| 测深精度 | 1 cm±0.1%×水深 |
构建潮间带高精度数字表面模型,首先使用大疆精灵4RTK无人机进行摄影测量,行高设置为100 m,航向重叠度为80%, 旁向重叠度为70%,获取航空相片641张。航测的同时在测区附近架设差分基准站进行静态数据采集,作为后处理差分的差分基准。最后利用连续运行参考站系统(continuously operating reference stations, CORS)获取差分基准站所在控制点的2000国家大地坐标系(CGCS2000)和1985国家高程。使用中海达IRTK5在潮间带附近获取特征点的三维坐标,作为无人机成果精度评定的标准,特征点位置如图1所示。
1.3 插值方法
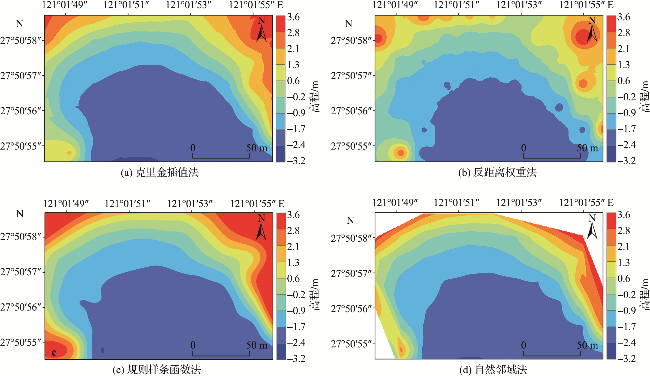
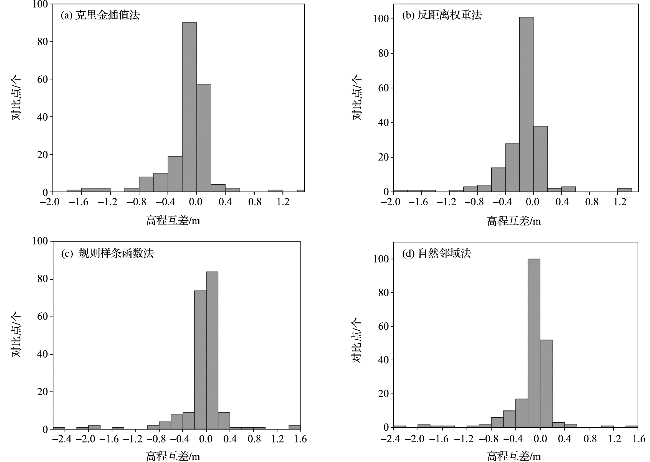
1.3.1 克里金插值法
克里金插值法是以变异函数理论分析为基础, 对有限区域内的区域化变量取值进行最优无偏估计的一种方法[15]。
其原理是假设研究区域高程变化量Z(xi) 满足二阶平稳假设和本征假设。 Z(xi)是一个二阶平稳的随机函数,在n个位置取样: Z(x1), Z(x2), …, Z(xn), 则点x0处的高程估计量为[16]
Z*(x0)= λiZ(xi)
式中:λi为权重系数,表示各空间已知点xi处的高程观测值Z(xi) 对x0处的高程估计值Z*(x0) 的影响程度。
克里金插值法在实际应用中需要设置较多的参数,首先需要创建变异函数和协方差函数估算取决于自相关模型的统计相关性值。本文选取球面函数作为变异函数模型,插值过程使用可变搜索半径。参考点数是用于执行插值的最邻近输入采样点数量的整数值,本试验中设为12。球面模型公式为
$\gamma(h)=\left\{\begin{array}{cc} 0 & h=0 \\ C_{0}+C\left(\frac{3 h}{2 a}-\frac{h^{3}}{2 a^{3}}\right) & (0<h \leqslant a) \\ C_{0}+C & h>a \end{array}\right. $
式中:γ(h)是待估点与已知点之间的空间自相关函数,h是待估点与已知点之间的空间距离。根据实测变换数据γ(hi),利用回归分析法求取球面模型系数C0、C、a,即可求出权重系数λi,然后根据式(1)求出待估点的高程。
1.3.2 反距离权重法
反距离权重法,也可以称为距离倒数乘方法,用于已知散点集的多变量插值,未知点分配值可用已知点坐标的加权平均值计算[17]。反距离权重法主要依赖于反距离的幂参数,幂参数可基于距输出点的距离来控制已知点对内插值的影响。幂参数是一个正实数,一般取值为0.5~3,本试验中幂参数设为2。插值过程中使用可变搜索半径,参考点数为12。
假设研究区域D内有n个点,则有每个已知点的权重U(x1,y1),U(x2,y2),…,U(xn,yn),反距离权重插值算法基本形式如下[17]
di=
$\lambda_{i}=\frac{1}{d_{i}\left(\sum_{i=1}^{n} \frac{1}{d_{i}}\right)} $
Un=U(xn,yn)= λiU(xi,yi)
式中:(x,y)为插值点, (xi,yi)为已知点,di是从已知点到插值点的给定距离 (度量算子), λi为插值点权重,n为用于插值的已知点总数。
1.3.3 规则样条函数法
样条函数法应用的插值方法是一种曲面重建方法,其值利用最小化表面总曲率的数学函数来估计,从而生成恰好经过输入点的平滑表面。于雪等[18]使用样条函数表示曲面梯度改进算法中的southwell模型,提高了曲面物体三维廓形模型的精度。样条函数法包括规则样条函数法与张力样条函数法,规则样条函数法相比张力样条函数法能够创建更为平滑的表面。由于本次研究区为潮间带,高程变化幅度较小,因此使用规则样条函数法进行插值。其基本原理是:存在一个假设的平面,当给该平面中某一点i赋予一个高程值时,以i为圆心,R为半径的区域内,与i点距离不同的各处将产生不同程度的垂直位移。
样条函数法使用以下公式进行插值:
S(x,y)=T(x,y)+ λiR(ri),i=1,2…,n
式中:S(x,y)为地形点预测值,T(x,y)表示以(x,y)为自变量的二元线性方程组,R(ri)表示以ri为自变量的方程,n为点数,λi是通过求解线性方程组而获得的系数,ri是点(x,y)到i点之间的距离。对于规则样条函数,
T(x,y)=a1+a2x+a3y
式中:a1,a2,a3是通过求解线性方程组而获得的系数,当a1+a2x+a3y=0时,即可求出λi。
$\begin{array}{c} R(r)=\frac{1}{2 \pi}\left\{\frac{r^{2}}{4}\left[\ln \left(\frac{r}{2 \tau}\right)+c-1\right]+\right. \\ \left.\tau^{2}\left[K_{0}\left(\frac{r}{\tau}\right)+c+\ln \left(\frac{r}{2 \pi}\right)\right]\right\} \end{array}$
式中:r是样本与插值点之间的距离; $\tau^{2}$是权重参数;K0是修正贝塞尔函数;c为常数,c=0.577 215。
权重参数$\tau^{2}$用于定义曲率最小化表达式中表面的三阶导数的权重,本次试验中权重参数$\tau^{2}$设为0.1,参考点数为12。
1.3.4 自然邻域法
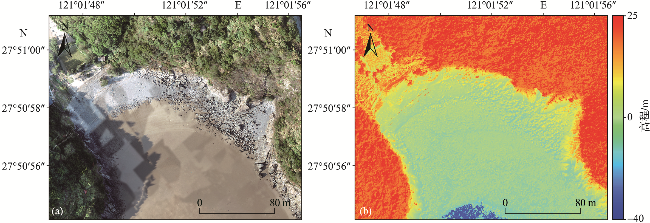
1.4 无人机摄影测量
利用无人机摄影测量拍摄的高分辨率照片能够快速生成测量地区的数字正射影像与数字表面模型。由于潮间带的地形不宜布设像控点,导致传统的无人机摄影测量精度降低,因此使用差分测量是必要的。而与实时动态差分(real-time kinematic,RTK)技术相比较,使用后处理差分(PPK)技术辅助无人机摄影测量能够解决实时数据链易断的问题,作业距离也显著增加。无人机PPK技术已经广泛应用于各种复杂地形的测量中,主要利用后处理差分基准站和流动站同步对GNSS卫星的载波相位进行观测,将接收到的数据在计算机中进行线性组合,结合后处理差分基准站已知坐标解算无人机的三维坐标。
2 结果与讨论
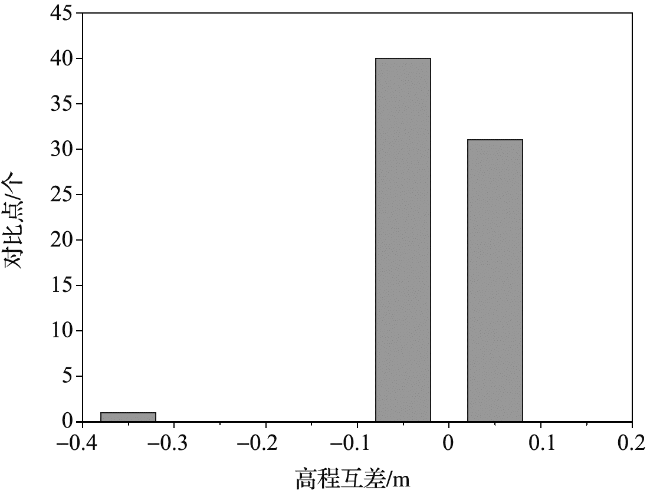
2.1 无人机潮间带摄影测量精度分析
PPK技术辅助无人机摄影测量建立的数字表面模型精度如表2所示。其中x方向的中误差为0.017 m,y方向的中误差为0.005 m,z方向的中误差为0.068 m。结果表明,PPK技术辅助无人机免像控航测成果满足1:500大比例尺测图要求。
表2 潮间带数字表面模型精度Tab.2 Accuracy of intertidal digital surface model |
| 特征点号/中误差 | △x/m | △y/m | △z/m |
|---|---|---|---|
| 1 | -0.009 | -0.001 | -0.083 |
| 2 | 0.022 | 0.002 | -0.018 |
| 3 | -0.013 | 0.003 | 0.057 |
| 4 | 0.016 | -0.004 | 0.033 |
| 5 | 0.020 | -0.011 | 0.041 |
| 6 | -0.016 | -0.004 | 0.098 |
| 中误差 | 0.017 | 0.005 | 0.068 |
2.2 单波束测深点位高程精度分析
单波束测深工作开始之前,在附近地形较为稳定的区域布设临时水位计,并测量出该水位计布放点的坐标,使用临时水位计的数据对单波束测深进行潮汐校正。单波束测深线由主测线和检查线组成,常规的数据检验方法是利用检查线对主测线进行核验。而利用无人机摄影测量构建潮间带的数字表面模型,可以检验主测线上所有的测量点。首先,在进行单波束测深时结合GNSS获取单波束测深点的三维坐标,测深点三维坐标的平面基准与高程基准应与无人机航测获取的潮间带数字表面模型的平面基准与高程基准保持一致;然后将单波束测深点与无人机获取的潮间带数字表面模型相叠加,提取出测深点在数字表面模型中的高程;最后将单波束测深点的原始高程与从无人机构建的数字表面模型中提取出的高程作差,得到测深点原始高程与提取出的高程之差。本文将两种高程之间的差距称为高程互差。对高程互差进行分析,本次试验中对比点共有72个,其中高程互差的绝对值在0.1 m以内的有71个对比点,占比99%,其中误差为0.046 m。只有一个点的原始高程与从无人机构建的数字表面模型中提取出的高程互差超过0.3 m,说明两种数据的符合性较好(高程互差的分布情况如图3所示)。
2.3 单波束测深插值结果分析
基于单波束测深数据与GNSS推算出水下地形点的三维坐标,平面基准基于CGCS2000,高程基准基于1985国家高程基准。分别使用克里金插值法、反距离函数法、规则样条函数法以及自然邻域法插值构建潮间带数字高程模型, 其结果如图4所示。
低潮时利用无人机摄影测量构建高精度潮间带数字表面模型,并随机均匀提取200个潮间带地形点。从4种插值方法构建的水下数字高程模型中提取对应坐标点的高程值进行高程互差对比分析(图5)。
陈长波等[4]建议对于水深值在20 m以内的数字水深模型,网格点水深值极限误差可设为0.4 m。本研究中潮间带的水深范围为0~2 m,因此将构建水下数字高程模型的极限误差值设为0.4 m。在无人机构建的数字表面模型中,在潮间带区域随机提取出200个地形点的平面坐标与高程值,利用这200个点的平面坐标将点投影到4种插值结果中,分别提取出插值结果中这200个点的高程值,求出两种高程值之差,即高程互差。由于本文构建水下数字高程模型的极限误差值设为0.4 m,因此将高程互差大于0.4 m的点视为带有粗差的点,带有粗差的点占全部点的比例称为粗差率。对比结果表明,基于克里金插值法构建的水下数字高程模型的粗差率为15%,反距离权重法的粗差率为15.5%,规则样条函数法的粗差率为12.5%,自然邻域法的粗差率为14%。
从粗差率可以看出,克里金插值法、反距离权重法、规则样条函数法以及自然邻域法的内插精度基本相当,但规则样条函数法的精度高于其他3种插值方法。反距离权重法的优势在于输入采样点足够密集时可以获得最佳结果,而本次试验中由单波束测深所获得的水下地形点较为稀疏,因此反距离权重法的粗差率在本次试验中最高。克里金插值法与反距离权重法类似,但克里金插值法在确定权重时,不仅取决于测量点之间的距离,也取决于整体测量点的空间排列。研究区域的潮间带三面环山,潮间带中部地势较低,三面较高,所以在插值过程中潮间带三面环山部分附近的点对插值精度的影响较大。自然邻域法是根据最近的输入样本子集,并基于区域大小分配权重,但该模型没有考虑到整体输入点的空间性,因此在本次试验中自然邻域法的粗差率略低于反距离权重法与克里金插值法,但不是最低。规则样条函数法利用最小化表面总曲率的数学函数来估计,从而生成恰好经过输入点的平滑表面。潮间带依据基底的性质,可分为岩礁、泥滩、沙滩及河口,此次研究区域中的潮间带底质为泥滩,且由于海水的冲刷使得其表面平滑,三面环山部分地势较高,中部地势较低,因此使用规则样条函数法插值,恰好可以生成一个与潮间带地形相贴近的曲面,所以在本次试验中规则样条函数法的粗差率最低。
总体来看,4种插值方法在地形起伏较小的潮间带数字高程模型构建中,都有较好的表现,而由于潮间带地形的特点,基于规则样条函数法所构建的模型精度最高。
3 结论
1)无人机免像控摄影测量在后处理差分技术的辅助下,可以构建高精度潮间带数字正射影像与数字表面模型。
2)在潮间带区域利用潮起潮落的规律,低潮时使用无人机获取潮间带高精度摄影测量数据可以作为高潮时单波束测深数据的检查标准,可以对全部由单波束测深所获得的水下地形点的高程进行精度评估。
3)以高精度无人机数据为基准,对由单波束测深数据换算而得的水下地形点进行插值,获取潮间带数字高程模型,并对插值模型进行精度分析可知,克里金插值法、反距离权重法、规则样条函数法以及自然邻域法精度相当且都能取得较好的表现,其中规则样条函数法插值精度最高。因此建议在地形平缓且开阔的泥质潮间带区域使用规则样条函数法进行插值。