基于独立样本的设计波高推算及其应用

doi:10.3969/j.issn.1001-909X.2023.03.007

摘要/Abstract

摘要：

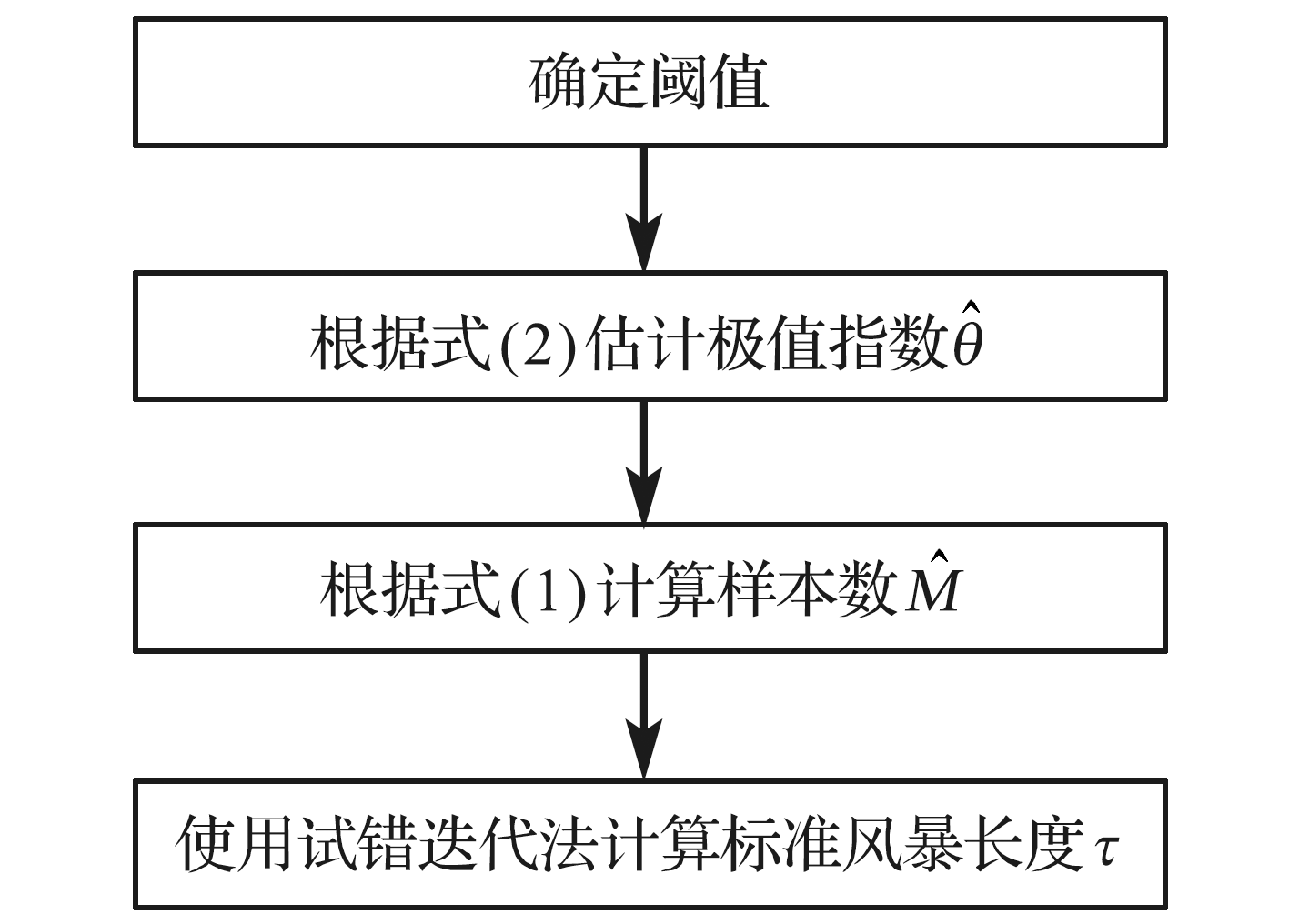
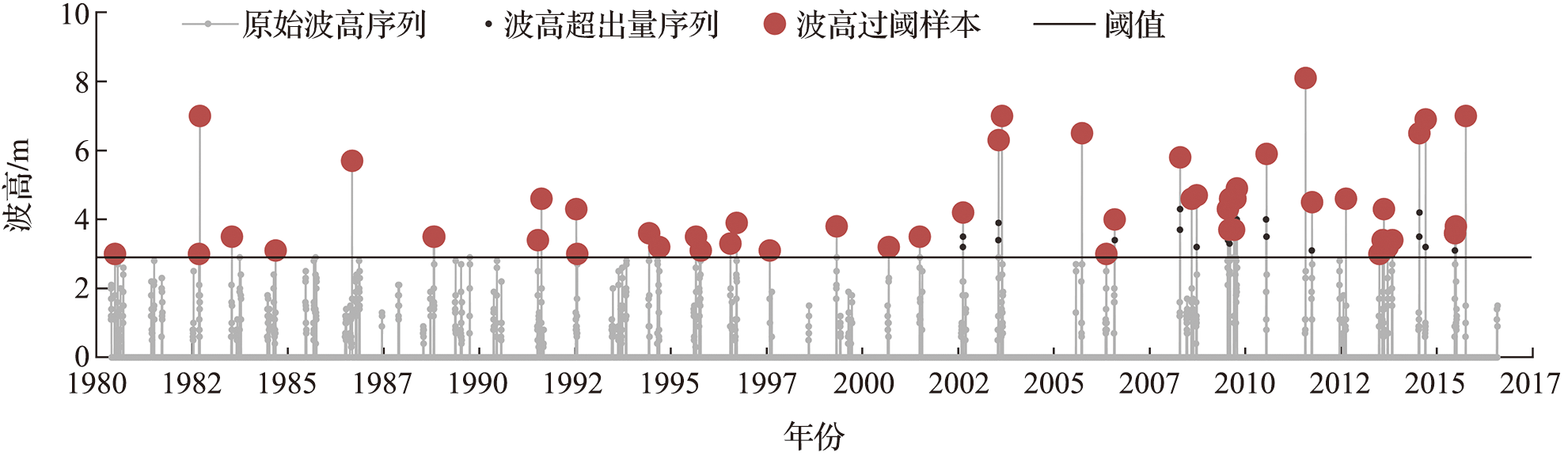
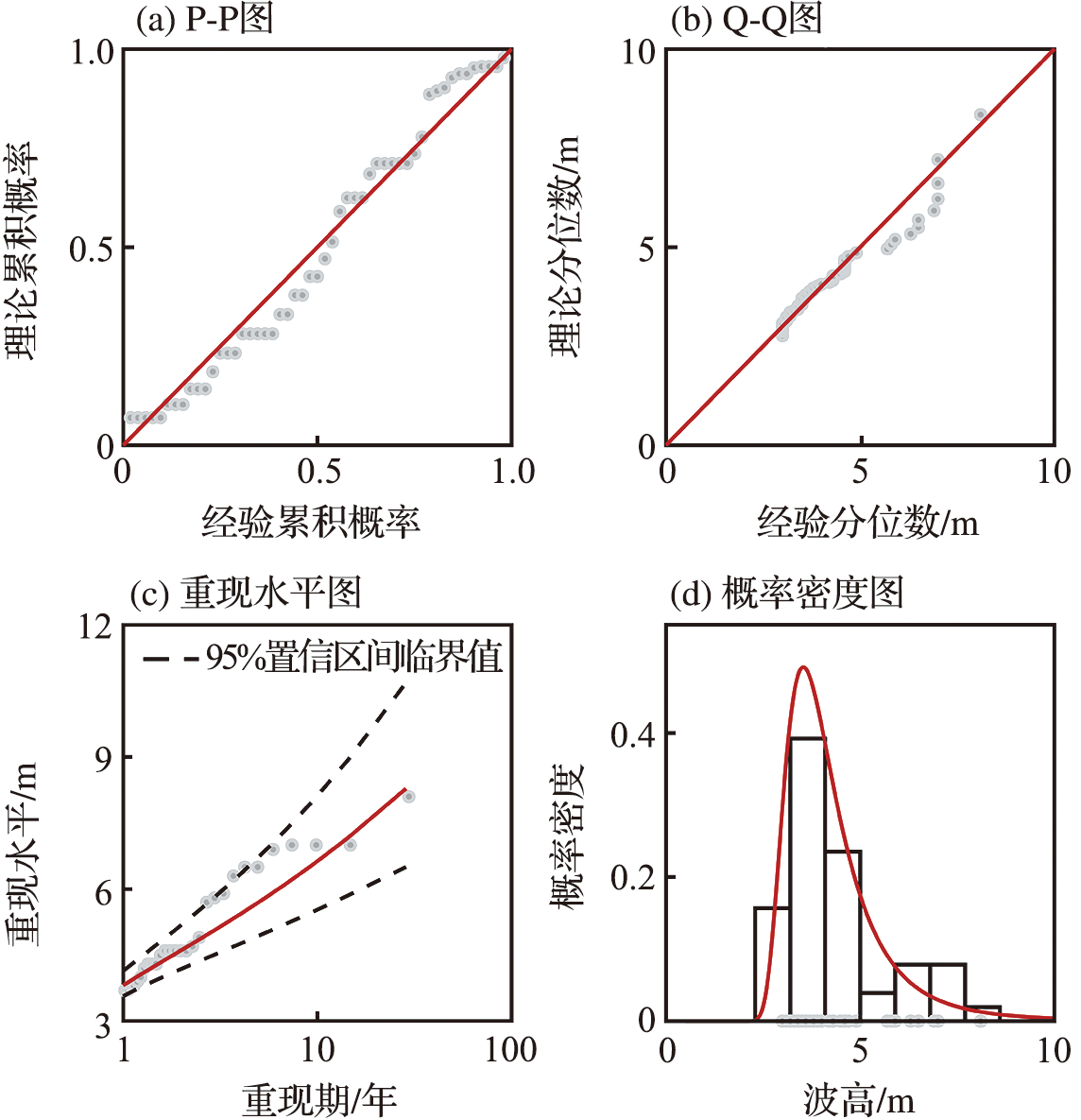
极值样本的选取和分布模型的确定是设计波高推算中的两个关键环节。使用阈值法选取波高过阈样本作为极值样本时,常用标准风暴长度法对超出量序列进行“去聚类”处理,以使样本符合独立性标准。然而标准风暴长度法中的标准风暴长度需要人为选择,增加了取样结果的不确定性。本文提出了一种自动的标准风暴长度估计方法,并基于该方法选取了粤西海域的波高过阈样本。波高过阈样本具有尖峰、厚尾的统计特征,为了更准确地拟合该样本,本文基于组合模型原理构建了一种新的分布模型——Gumbel-Pareto分布模型,并用该模型进行了粤西海域的设计波高推算,结果表明Gumbel-Pareto分布对波高过阈样本的拟合优度比Gumbel分布和广义Pareto分布更高,可以为大型海洋工程设计波高的确定提供参考。

关键词: 独立样本, 标准风暴长度, Gumbel-Pareto分布, 设计波高推算

Abstract:

The selection of extreme value samples and the determination of distribution models are two crucial aspects when calculating the design wave height. When selecting extreme value samples using the peaks over threshold method, the standard storm length method is commonly used to “de-cluster” the exceedances in order to make the samples conform to independence standards. However, the crucial parameter in the standard storm length method needs to be manually selected which increases the uncertainty of samples. In this paper, an automatic standard storm length estimation method is proposed, then the wave height peaks over threshold sample in the western Guangdong sea area is selected based on this method. To accurately fit the sharp peak and heavy tail of the wave height peaks over threshold sample, the combined distribution method is used to construct a new model: Gumbel-Pareto distribution model. Based on this model, the design wave height calculation is carried out in the western Guangdong sea area. The result shows that the goodness of fit for the Gumbel-Pareto distribution model to the wave height peaks over threshold sample is higher than that of Gumbel distribution and Generalized Pareto distribution, which can offer a reasonable reference for the design of large offshore engineering.

Key words: independent samples, standard storm length, Gumbel-Pareto distribution, design wave height calculation

中图分类号:

P731.22

刘桂林, 房丹, 宋时春, 刘泊湖. 基于独立样本的设计波高推算及其应用[J]. 海洋学研究, 2023, 41(3): 73-82.

LIU Guilin, FANG Dan, SONG Shichun, LIU Bohu. Calculation of design wave height and its application base on independent sample[J]. Journal of Marine Sciences, 2023, 41(3): 73-82.

图/表 10

图1 自动的标准风暴长度估计方法

Fig.1 Procedures for automated standard storm length estimation

图2 Gumbel-Pareto分布的p.d.f.曲线

Fig.2 The p.d.f. curves of Gumbel-Pareto distribution

图3 日最大波高数据的平均剩余量图(a)和GPD参数图(b,c)

Fig.3 Mean excess plot (a) and GPD parameters’ stability plot (b,c) of wave height daily maxima data

图4 原始波高序列、波高超出量序列、波高过阈样本及阈值

Fig.4 Original wave height series, wave height exceedences, wave height peaks over threshold sample and the threshold

图5 原始波高序列(a)和波高过阈样本(b)的自相关图

Fig.5 Autocorrelation plot of original wave height series (a) and wave height peaks over threshold sample (b)

表1 样本的主要统计特征量

Tab.1 Main statistical characteristics of samples

样本	尾部指数	均值/m	方差/m²	偏度/m³	峰度/m³
波高过阈样本	3.059	4.351	1.798	1.092	3.124
波高年极值样本	9.958	4.610	2.611	0.437	2.354

表2 分布参数估计及K-S检验结果

Tab.2 Results of parameters’ estimation and K-S tests

样本	分布模型	参数	参数估计值	K-S检验的p值
波高过阈样本	Gumbel-Pareto 分布	β	2.839	0.807
		α	1.695
		σ	3.677
	Gumbel 分布	尺度	0.894	0.419
	Gumbel 分布	位置	3.772	0.419
	GPD	形状	0.076	0.322
		尺度	2.120
		位置	2.900
波高年极值样本	Gumbel-Pareto 分布	β	2.497	0.305
		α	0.970
		σ	3.584
	Gumbel 分布	尺度	1.362	0.689
	Gumbel 分布	位置	3.855	0.689
	GPD	形状	0.268	0.272
		尺度	3.110
		位置	1.500

图6 Gumbel-Pareto分布对波高过阈样本的拟合优度检验图

Fig.6 Goodness of fit test plot of Gumbel-Pareto distribution for wave height peaks over threshold sample

图7 波高过阈样本直方图及不同分布的p.d.f.曲线

Fig.7 Histogram of the wave height peaks over threshold sample and p.d.f. curves of different distributions

表3 不同分布模型计算的20年、50年、100年和500年一遇设计波高

Tab.3 20-, 50-,100-, 500-year return levels of design wave height calculated by different distribution models

重现期/年	设计波高/m
重现期/年	Gumbel-Pareto分布	Gumbel分布	GPD
20	6.037	5.904	7.646
50	7.346	6.748	10.060
100	8.500	7.376	11.990
500	11.890	8.821	16.910

参考文献 35

[1]	LIU G L, LI X, WANG J H, et al. Research on the statistical characteristics of typhoon frequency[J]. Ocean Engineering, 2020, 209: 107489. DOI URL
[2]	殷玉齐, 侯一筠, 冯兴如, 等. 汕尾市引发灾害性海浪的热带气旋特征研究[J]. 海洋与湖沼, 2021, 52(1):66-74.
	YIN Y Q, HOU Y J, FENG X R, et al. Characteristics of tropical cyclones that cause disastrous waves in Shanwei city[J]. Oceanologia et Limnologia Sinica, 2021, 52(1): 66-74.
[3]	自然资源部海洋预警监测司. 2019年中国海洋灾害公报[EB/OL].(2020-05-20) [2022-09-25]. http://www.nmdis.org.cn/hygb/zghyzhgb/2019nzghyzhgb/.
	Marine Early Warning and Monitoring Division of the Ministry of Natural Resources. Bulletin of China marine disaster in 2019[EB/OL].(2020-05-20) [2022-09-25]. http://www.nmdis.org.cn/hygb/zghyzhgb/2019nzghyzhgb/.
[4]	潘冬冬, 周川, 王俊, 等. 粤东近岸深水区周年波浪特征分析[J]. 南方能源建设, 2020, 7(4):34-40.
	PAN D D, ZHOU C, WANG J, et al. Analysis of the annual wave characteristics in the deep water area near the east coast of Guangdong Province[J]. Southern Energy Construction, 2020, 7(4): 34-40.
[5]	CHEN B Y, KOU Y, WANG Y F, et al. Analysis of storm surge characteristics based on stochastic process[J]. AIMS Mathematics, 2021, 6(2): 1177-1190. DOI URL
[6]	SHAO Z X, LIANG B C, LI H J, et al. Study of sampling methods for assessment of extreme significant wave heights in the South China Sea[J]. Ocean Engineering, 2018, 168: 173-184. DOI URL
[7]	LIU G L, YU Y H, KOU Y, et al. Joint probability analysis of marine environmental elements[J]. Ocean Engineering, 2020, 215: 107879. DOI URL
[8]	WANG L P, XU X, LIU G L, et al. A new method to estimate wave height of specified return period[J]. Chinese Journal of Oceanology and Limnology, 2017, 35(5): 1002-1009. DOI URL
[9]	TAWN J A. An extreme-value theory model for dependent observations[J]. Journal of Hydrology, 1988, 101(1-4): 227-250. DOI URL
[10]	SIMIU E, HECKERT N A. Extreme wind distribution tails: A “peaks over threshold” approach[J]. Journal of Structural Engineering, 1996, 122(5): 539-547. DOI URL
[11]	李晓恩. 超阈法-Copula函数在极端水位重现期值计算中的应用研究[D]. 广州: 华南理工大学, 2020.
	LI X E. Research on POT-Copula method in the calculation of extreme water level and its application[D]. Guangzhou: South China University of Technology, 2020.
[12]	KIRAN K G, SRINIVAS V V. A mahalanobis distance-based automatic threshold selection method for peaks over threshold model[J]. Water Resources Research, 2021, 57(1): e2020WR027534.
[13]	DING J, CHEN X Z. Assessment of methods for extreme value analysis of non-Gaussian wind effects with short-term time history samples[J]. Engineering Structures, 2014, 80: 75-88. DOI URL
[14]	GUEDES SOARES C, SCOTTO M G. Application of the r largest-order statistics for long-term predictions of significant wave height[J]. Coastal Engineering, 2004, 51(5/6): 387-394. DOI URL
[15]	GAO H J, WANG L Q, LIANG B C, et al. Estimation of extreme significant wave heights in the Yellow Sea, China[C]// Proceedings of the 28th International Ocean and Polar Engineering Conference.[S.l.]: ISOPE, 2018: 387-391.
[16]	CHAPON A, HAMDI Y. A bivariate nonstationary extreme values analysis of skew surge and significant wave height in the English channel[J]. Atmosphere, 2022, 13(11): 1795. DOI URL
[17]	HALTAS I. Estimating extreme high still water levels in North San Francisco Bay: Comparison of annual maxima method with direct and indirect methods[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2022, 148(1): 04021040.
[18]	MARKOVICH N. Nonparametric analysis of univariate heavy-tailed data: Research and practice[M]. New York: Wiley, 2007.
[19]	LIU G L, NIE C, KOU Y, et al. Elevation calculation of bottom deck based on stochastic process and compound distribution[J]. Journal of Marine Science and Engineering, 2021, 9(7): 697. DOI URL
[20]	史道济. 实用极值统计方法[M]. 天津: 天津科学技术出版社, 2006:8-70.
	SHI D J. Practical extreme value statistical method[M]. Tianjin: Tianjin Scientific & Technical Publishers, 2006: 8-70.
[21]	CHEN B Y, KOU Y, WU F, et al. Study on evaluation standard of uncertainty of design wave height calculation model[J]. Journal of Oceanology and Limnology, 2021, 39(4): 1188-1197. DOI
[22]	CHEN B Y, KOU Y, ZHAO D, et al. Maximum entropy distribution function and uncertainty evaluation criteria[J]. China Ocean Engineering, 2021, 35(2): 238-249. DOI
[23]	HU Y, SCARROTT C. evmix: An R package for extreme value mixture modeling, threshold estimation and boundary corrected kernel density estimation[J]. Journal of Statistical Software, 2018, 84(5): 1-27.
[24]	BEHRENS C N, LOPES H F, GAMERMAN D. Bayesian analysis of extreme events with threshold estimation[J]. Statistical Modelling, 2004, 4(3): 227-244. DOI URL
[25]	CARREAU J, BENGIO Y. A hybrid Pareto model for asymmetric fat-tailed data: The univariate case[J]. Extremes, 2009, 12(1): 53-76. DOI URL
[26]	LI C, SINGH V P, MISHRA A K. Simulation of the entire range of daily precipitation using a hybrid probability distribution[J]. Water Resources Research, 2012, 48(3): W03521.
[27]	MEKONNEN B A, NAZEMI A, MAZUREK K A, et al. Hybrid modelling approach to prairie hydrology: Fusing data-driven and process-based hydrological models[J]. Hydrological Sciences Journal, 2015, 60(9): 1473-1489. DOI URL
[28]	FURRER E M, KATZ R W. Improving the simulation of extreme precipitation events by stochastic weather generators[J]. Water Resources Research, 2008, 44(12): W12439.
[29]	LEADBETTER M R. Extremes and local dependence in stationary sequences[J]. Zeitschrift für Wahrschein-lichkeitstheorie und Verwandte Gebiete, 1983, 65(2): 291-306.
[30]	FERRO C A T, SEGERS J. Inference for clusters of extreme values[J]. Journal of the Royal Statistical Society Series B: Statistical Methodology, 2003, 65(2): 545-556. DOI URL
[31]	ALZAATREH A, LEE C, FAMOYE F. A new method for generating families of continuous distributions[J]. METRON, 2013, 71(1): 63-79. DOI URL
[32]	LIU G L, CUI K, JIANG S, et al. A new empirical distribution for the design wave heights under the impact of typhoons[J]. Applied Ocean Research, 2021, 111: 102679. DOI URL
[33]	LIU G L, GAO Z K, CHEN B Y, et al. Study on threshold selection methods in calculation of ocean environmental design parameters[J]. IEEE Access, 2019, 7: 39515-39527. DOI URL
[34]	MANDELBROT B B. The variation of certain speculative prices[M]//Fractals and scaling in finance. New York: Springer, 1997: 371-418.
[35]	MARINHO P R D, SILVA R B, BOURGUIGNON M, et al. Adequacy Model: An R package for probability distributions and general purpose optimization[J]. PLoS One, 2019, 14(8): e0221487.