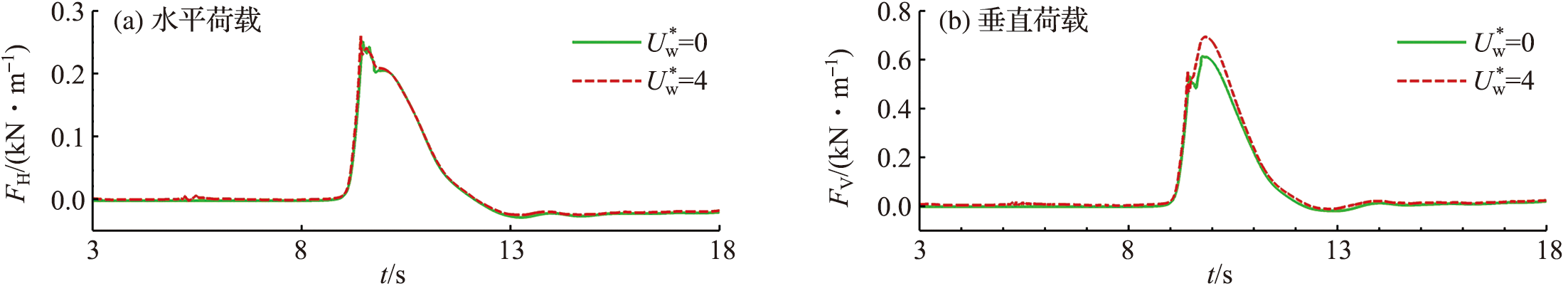风对孤立波海堤越浪特性影响的数值模拟研究

doi:10.3969-j.issn.1001-909X.2023.04.004

海洋学研究 ›› 2023, Vol. 41 ›› Issue (4): 32-45.DOI: 10.3969-j.issn.1001-909X.2023.04.004

风对孤立波海堤越浪特性影响的数值模拟研究

张良斌¹(), 屈科¹^,²^,³^,^*(), 黄竞萱¹, 王旭¹, 虢磊¹

1.长沙理工大学水利与环境工程学院,湖南长沙 410114
2.洞庭湖水环境治理与生态修复湖南省重点实验室,湖南长沙 410114
3.水沙科学与水灾害防治湖南省重点实验室,湖南长沙 410114

收稿日期:2023-02-10 修回日期:2023-10-23 出版日期:2023-12-15 发布日期:2024-01-30
通讯作者: *屈科(1985—),男,副教授,主要从事计算水动力学、海洋/海岸多尺度流动方面的研究,E-mail:kqu@csust.edu.cn。
作者简介:张良斌(1995—),男,安徽省黄山市人,主要从事波浪与结构物相互作用方面的研究,E-mail:zlb1316675006@163.com。
基金资助:
国家重点研发计划(2022YFC3103601);国家自然科学基金重点项目(51839002);湖南省自然科学基金项目(2021JJ20043)

Numerical simulation study on influences of onshore wind on overtopping characteristics of solitary wave under coastal seawall

ZHANG Liangbin¹(), QU Ke¹^,²^,³^,^*(), HUANG Jingxuan¹, WANG Xu¹, GUO Lei¹

1. School of Hydraulic and Environmental Engineering, Changsha University of Science & Technology, Changsha410114, China
2. Key Laboratory of Dongting Lake Aquatic Eco-Environmental Control and Restoration of Hunan;Province, Changsha 410114, China
3. Key Laboratory of Water-Sediment Sciences and Water Disaster Preventionof Hunan Province, Changsha 410114, China

Received:2023-02-10 Revised:2023-10-23 Online:2023-12-15 Published:2024-01-30

摘要/Abstract

摘要：

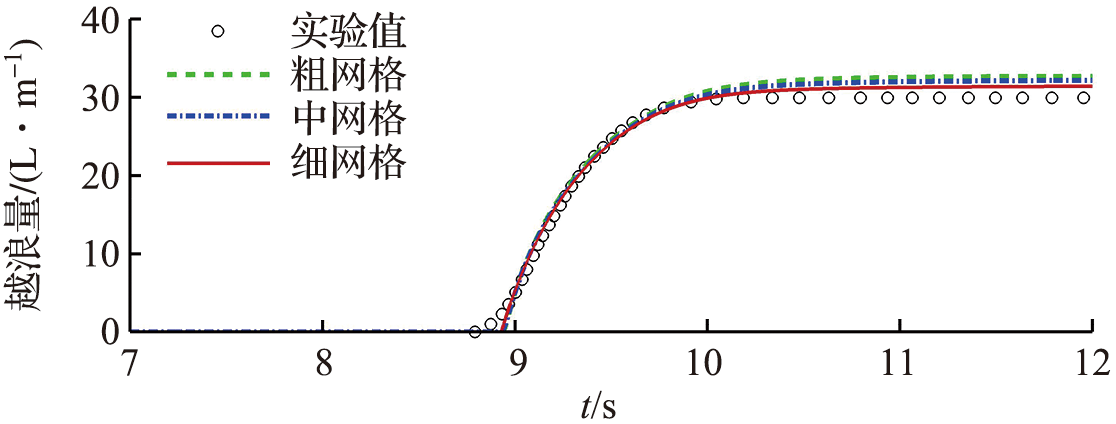
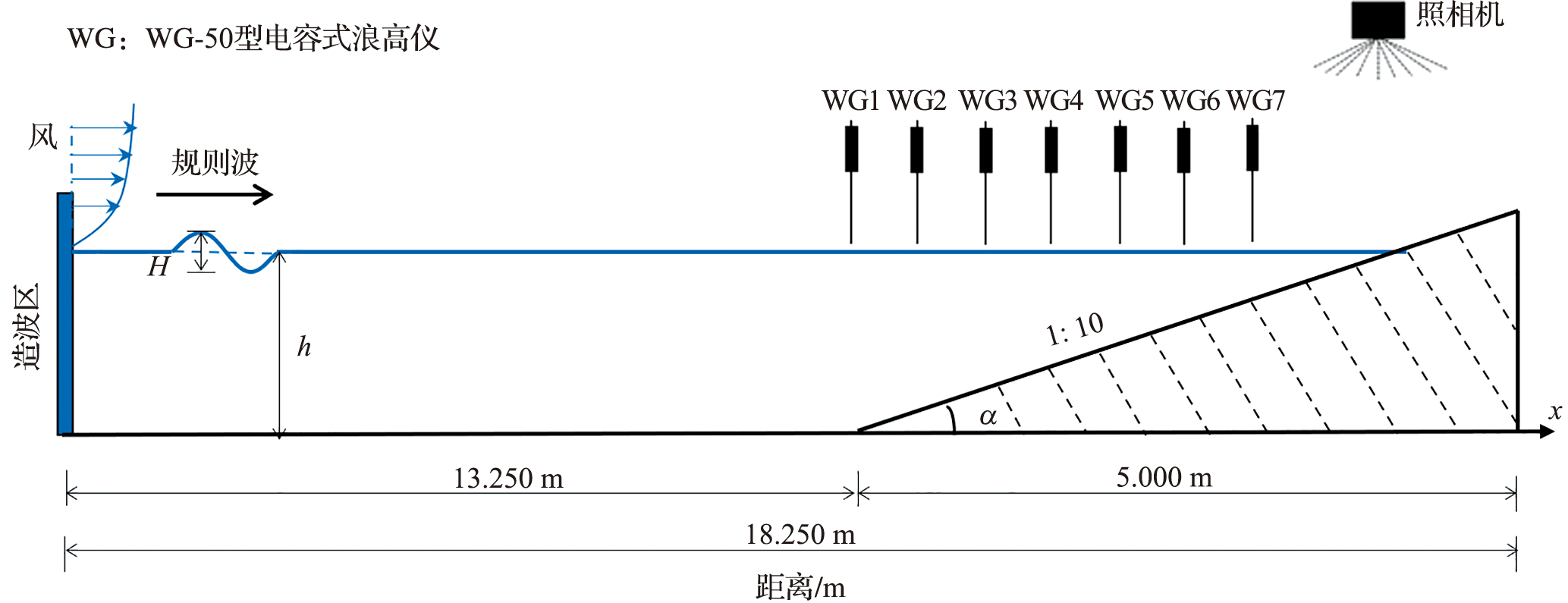
海堤在保护沿海城镇免受极端波浪破坏方面具有重要作用。该文基于二维不可压缩两相流数值模型,系统研究了向岸风对孤立波海堤越浪特性的影响。通过数值计算结果与实验数据的对比,验证了该数值模型的可靠性,并重点讨论了向岸风风速、入射波高、堤顶超高、岸滩坡度和海堤坡度等因素对孤立波海堤越浪水动力过程的影响。研究表明:随着向岸风风速、入射波高的增大以及堤顶超高的减小,孤立波的最大越浪量、最大爬高以及沿程最大水位高程逐渐增大;随着岸滩坡度和海堤坡度的增大,孤立波的最大越浪量分别增大和减小,最大爬高逐渐增大。向岸风会影响孤立波海堤越浪的水动力特性,增大孤立波的波陡以及波峰传播速度,使波浪提前破碎;相比无风情况,最大越浪量、最大爬高、最大水动力荷载以及沿程最大水位高程均有所增大。研究结果可为海岸工程的设计提供参考。

关键词: 孤立波, 向岸风, 越浪量, 数值模拟, 水动力特性

Abstract:

Seawalls play an important role in protecting coastal towns from extreme waves damage. Based on two-dimensional incompressible two-phase flow numerical model, the influences of onshore wind on overtopping characteristics of solitary wave under coastal seawall were systematically studied in this paper. The reliability of the numerical model was verified by comparing the numerical results with experimental data, and the influencing factors such as onshore wind speed, incident wave height, crest freeboards of the coastal seawall, beach slope and seawall slope on the hydrodynamic process of solitary wave overtopping of coastal seawalls were discussed in detail. The research results show that with the increase of onshore wind speed, incident wave height and the decrease of crest freeboards of the coastal seawall, the maximum overtopping volume, maximum runup height and spatial distributions of the maximum water elevation gradually increase. With the increase of beach slope and seawall slope, the maximum overtopping volume increase and decrease, respectively, while the maximum runup height gradually increase. Onshore wind can affect the hydrodynamic characteristics of solitary wave overtopping of coastal seawall, increase the wave steepness and the wave crest propagation speed and cause the wave breaking earlier. Compared with the windless condition, the maximum wave overtopping volume, maximum runup height, maximum hydrodynamic forces and spatial distributions of the maximum water elevation are increased under onshore wind. The results of this study can provide a reference for the design of coastal engineering.

Key words: solitary wave, onshore wind, overtopping volume, numerical simulation, hydrodynamic characteristics

中图分类号:

张良斌, 屈科, 黄竞萱, 王旭, 虢磊. 风对孤立波海堤越浪特性影响的数值模拟研究[J]. 海洋学研究, 2023, 41(4): 32-45.

ZHANG Liangbin, QU Ke, HUANG Jingxuan, WANG Xu, GUO Lei. Numerical simulation study on influences of onshore wind on overtopping characteristics of solitary wave under coastal seawall[J]. Journal of Marine Sciences, 2023, 41(4): 32-45.

图/表 28

图1 实验区域布置图[11]

Fig.1 Experimental layout[11]

图2 不同测点处的波高时程曲线

Fig.2 The temporal evolution of wave height for different wave gauges

图3 不同时刻的沿程水位高程空间分布

Fig.3 Spatial distributions of wave elevation at different times

图4 孤立波的时程越浪量

Fig.4 The temporal evolution of solitary wave overtopping volume

图5 实验区域布置图[28]

Fig.5 Experimental layout[28]

图6 不同测点处的波高时程曲线

Fig.6 The temporal evolution of wave height for different wave gauges

图7 计算区域布置图

Fig.7 Computational layout

表1 数值模拟工况和波浪破碎类型

Tab.1 Parameter setup of numerical simulation and wave breaking types

工况	$U w *$	H/m	A_C/m	cotα	cotβ	破碎类型	工况	$U w *$	H/m	A_C/m	cotα	cotβ	破碎类型
1	0	0.10	0.117	20	2	卷破波	23	4	0.10	0.067	20	2	卷破波
2	1	0.10	0.117	20	2	卷破波	24	0	0.10	0.117	10	2	激破波
3	2	0.10	0.117	20	2	卷破波	25	4	0.10	0.117	10	2	激破波
4	3	0.10	0.117	20	2	卷破波	26	0	0.10	0.117	15	2	卷破波
5	4	0.10	0.117	20	2	卷破波	27	4	0.10	0.117	15	2	卷破波
6	5	0.10	0.117	20	2	卷破波	28	0	0.10	0.117	20	2	卷破波
7	6	0.10	0.117	20	2	卷破波	29	4	0.10	0.117	20	2	卷破波
8	0	0.05	0.117	20	2	卷破波	30	0	0.10	0.117	25	2	卷破波
9	4	0.05	0.117	20	2	卷破波	31	4	0.10	0.117	25	2	卷破波
10	0	0.10	0.117	20	2	卷破波	32	0	0.10	0.117	30	2	卷破波
11	4	0.10	0.117	20	2	卷破波	33	4	0.10	0.117	30	2	卷破波
12	0	0.15	0.117	20	2	卷破波	34	0	0.10	0.117	20	0	卷破波
13	4	0.15	0.117	20	2	卷破波	35	4	0.10	0.117	20	0	卷破波
14	0	0.20	0.117	20	2	卷破波	36	0	0.10	0.117	20	1	卷破波
15	4	0.20	0.117	20	2	卷破波	37	4	0.10	0.117	20	1	卷破波
16	0	0.10	0.217	20	2	卷破波	38	0	0.10	0.117	20	2	卷破波
17	4	0.10	0.217	20	2	卷破波	39	4	0.10	0.117	20	2	卷破波
18	0	0.10	0.167	20	2	卷破波	40	0	0.10	0.117	20	3	卷破波
19	4	0.10	0.167	20	2	卷破波	41	4	0.10	0.117	20	3	卷破波
20	0	0.10	0.117	20	2	卷破波	42	0	0.10	0.117	20	4	卷破波
21	4	0.10	0.117	20	2	卷破波	43	4	0.10	0.117	20	4	卷破波
22	0	0.10	0.067	20	2	卷破波

表1 数值模拟工况和波浪破碎类型

Tab.1 Parameter setup of numerical simulation and wave breaking types

工况	$U w *$	H/m	A_C/m	cotα	cotβ	破碎类型	工况	$U w *$	H/m	A_C/m	cotα	cotβ	破碎类型
1	0	0.10	0.117	20	2	卷破波	23	4	0.10	0.067	20	2	卷破波
2	1	0.10	0.117	20	2	卷破波	24	0	0.10	0.117	10	2	激破波
3	2	0.10	0.117	20	2	卷破波	25	4	0.10	0.117	10	2	激破波
4	3	0.10	0.117	20	2	卷破波	26	0	0.10	0.117	15	2	卷破波
5	4	0.10	0.117	20	2	卷破波	27	4	0.10	0.117	15	2	卷破波
6	5	0.10	0.117	20	2	卷破波	28	0	0.10	0.117	20	2	卷破波
7	6	0.10	0.117	20	2	卷破波	29	4	0.10	0.117	20	2	卷破波
8	0	0.05	0.117	20	2	卷破波	30	0	0.10	0.117	25	2	卷破波
9	4	0.05	0.117	20	2	卷破波	31	4	0.10	0.117	25	2	卷破波
10	0	0.10	0.117	20	2	卷破波	32	0	0.10	0.117	30	2	卷破波
11	4	0.10	0.117	20	2	卷破波	33	4	0.10	0.117	30	2	卷破波
12	0	0.15	0.117	20	2	卷破波	34	0	0.10	0.117	20	0	卷破波
13	4	0.15	0.117	20	2	卷破波	35	4	0.10	0.117	20	0	卷破波
14	0	0.20	0.117	20	2	卷破波	36	0	0.10	0.117	20	1	卷破波
15	4	0.20	0.117	20	2	卷破波	37	4	0.10	0.117	20	1	卷破波
16	0	0.10	0.217	20	2	卷破波	38	0	0.10	0.117	20	2	卷破波
17	4	0.10	0.217	20	2	卷破波	39	4	0.10	0.117	20	2	卷破波
18	0	0.10	0.167	20	2	卷破波	40	0	0.10	0.117	20	3	卷破波
19	4	0.10	0.167	20	2	卷破波	41	4	0.10	0.117	20	3	卷破波
20	0	0.10	0.117	20	2	卷破波	42	0	0.10	0.117	20	4	卷破波
21	4	0.10	0.117	20	2	卷破波	43	4	0.10	0.117	20	4	卷破波
22	0	0.10	0.067	20	2	卷破波

图8 有风和无风时不同时刻水体的速度云图

Fig.8 Velocity contours of water body at different time moments in windy and windless conditions

图9 有风和无风时孤立波爬高(a)和越浪量(b)时程曲线对比

Fig.9 Comparison of the time series of solitary wave runup height (a) and volume of overtopping water (b) in windy and windless conditions

图10 有风和无风时海堤所受的水动力荷载

Fig.10 Hydrodynamic forces exerted at the seawall in windy and windless conditions

图11 有风和无风时沿程最大水位高程空间分布

Fig.11 Spatial distributions of the maximum water elevation in windy and windless conditions

图12 有风(a)和无风(b)时的湍流剪切应力对比

Fig.12 Comparison of turbulent shear stress between windy (a) and windless (b) conditions

图13 不同风速下孤立波的最大爬高(a)和最大越浪量(b)

Fig.13 Maximum runup height (a) and maximum overtopping volume (b) of solitary wave under different onshore wind speeds

图14 不同风速下不同测点处相对波高的比较

Fig.14 Comparison of relative wave height for different wave gauges under different onshore wind speeds

图15 不同风速下沿程最大水位高程空间分布

Fig.15 Spatial distributions of the maximum water elevation under different onshore wind speeds

图16 不同入射波高下有风和无风时孤立波的最大爬高(a)和最大越浪量(b)

Fig.16 Maximum value of runup height (a) and maximum overtopping volume (b) of solitary wave in windy and windless conditions under different incident wave heights

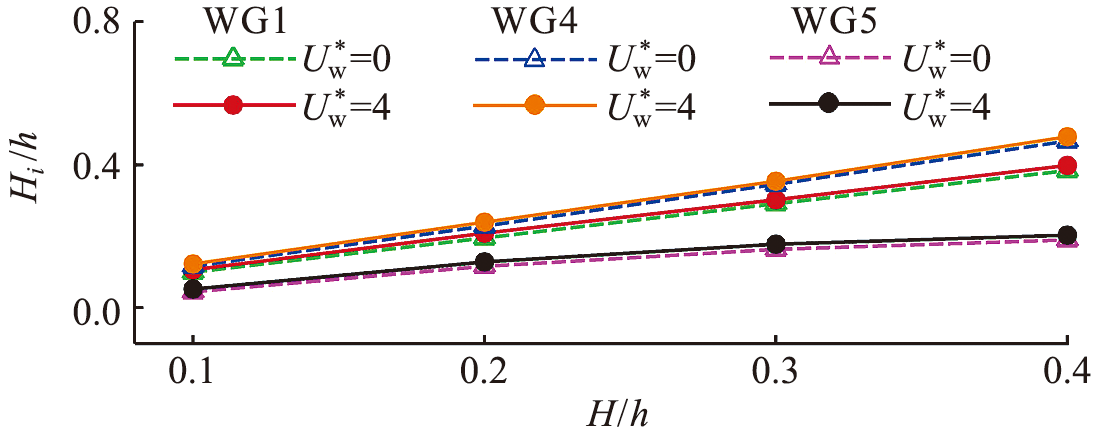
图17 不同入射波高下有风和无风时不同测点处相对波高的比较

Fig.17 Comparison of relative wave height for different wave gauges in windy and windless conditions under different incident wave heights

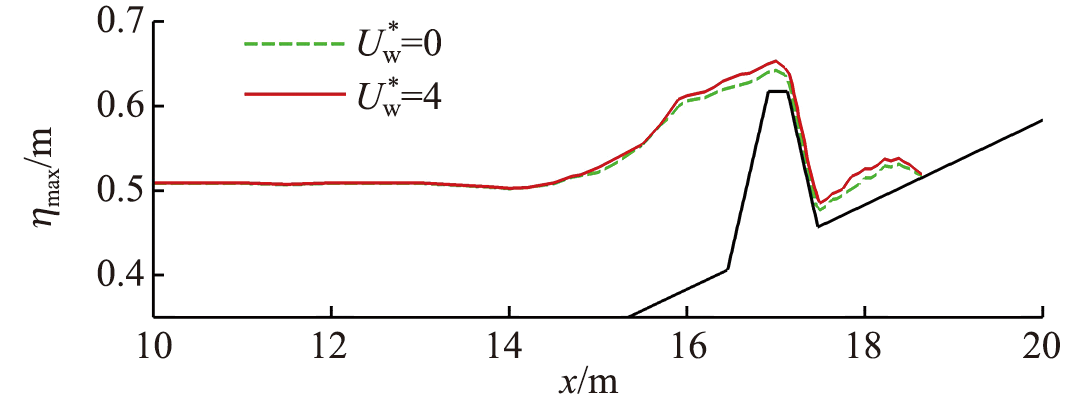
图18 不同入射波高下有风和无风时沿程最大水位高程空间分布

Fig.18 Spatial distributions of the maximum water elevation in windy and windless conditions under different incident wave heights

图19 不同堤顶超高下有风和无风时孤立波的最大爬高(a)和最大越浪量(b)

Fig.19 Maximum value of runup height (a) and maximum overtopping volume (b) of solitary wave in windy and windless conditions under different dimensionless crest freeboards

图20 不同堤顶超高下有风和无风时不同测点处相对波高的比较

Fig.20 Comparison of relative wave height for different wave gauges in windy and windless conditions under different dimensionless crest freeboards

图21 不同堤顶超高下有风和无风时沿程最大水位高程空间分布

Fig.21 Spatial distributions of the maximum water elevation in windy and windless conditions under different dimensionless crest freeboards

图22 不同岸滩坡度下有风和无风时孤立波的最大爬高(a)和最大越浪量(b)

Fig.22 Maximum value of runup height (a) and maximum overtopping volume (b) of solitary wave in windy and windless conditions under different beach slopes

图23 不同岸滩坡度下有风和无风时不同测点处相对波高的比较

Fig.23 Comparison of relative wave height for different wave gauges in windy and windless conditions under different beach slopes

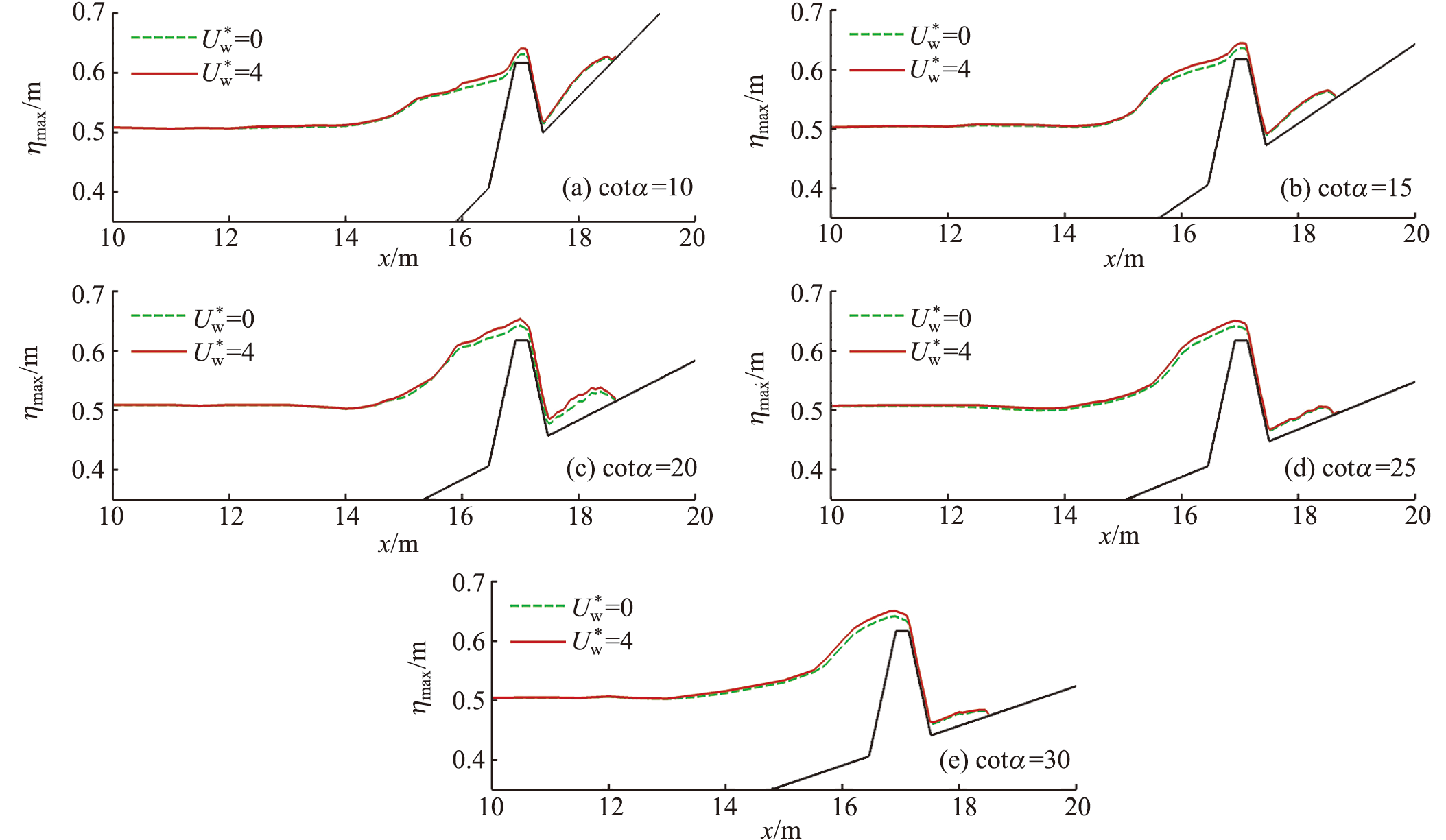
图24 不同岸滩坡度下有风和无风时沿程最大水位高程空间分布

Fig.24 Spatial distributions of the maximum water elevation in windy and windless conditions under different beach slopes

图25 不同海堤坡度下有风和无风时孤立波的最大爬高(a)和最大越浪量(b)

Fig.25 Maximum value of runup height (a) and maximum overtopping volume (b) of solitary wave in windy and windless conditions under different seawall slopes

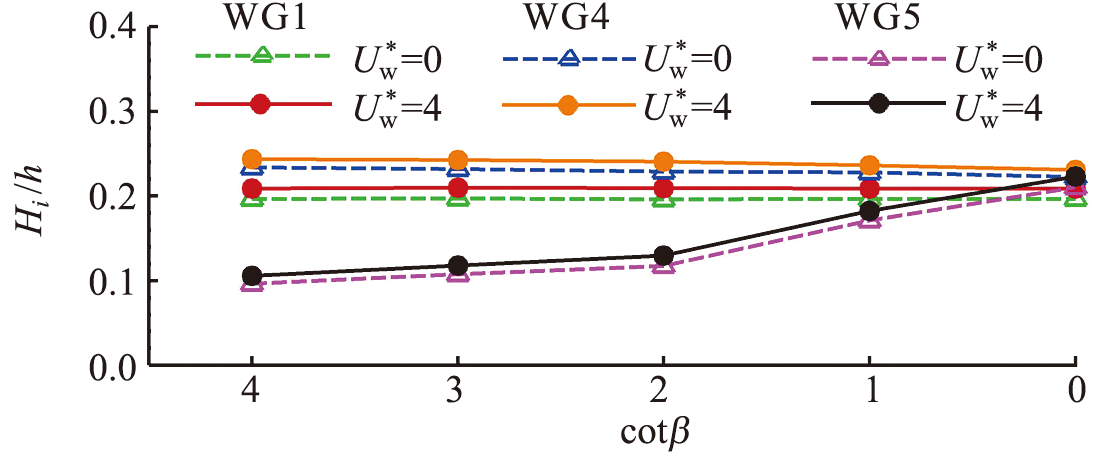
图26 不同海堤坡度下有风和无风时不同测点处相对波高的比较

Fig.26 Comparison of relative wave height for different wave gauges in windy and windless conditions under different seawall slopes

图27 不同海堤坡度下有风和无风时沿程最大水位高程空间分布

Fig.27 Spatial distributions of the maximum water elevation in windy and windless conditions under different seawall slopes

参考文献 29

[1]	CHO Y S, PARK K Y, LIN T H. Run-up heights of nearshore tsunamis based on quadtree grid system[J]. Ocean Engineering, 2004, 31(8/9): 1093-1109. DOI URL
[2]	SYNOLAKIS C E, BERNARD E N. Tsunami science before and beyond Boxing Day 2004[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2006, 364(1845): 2231-2265. DOI URL
[3]	姚远, 蔡树群, 王盛安. 海啸波数值模拟的研究现状[J]. 海洋科学进展, 2007, 25(4):487-494.
	YAO Y, CAI S Q, WANG S A. Present status of study on numerical simulation of tsunami wave[J]. Advances in Marine Science, 2007, 25(4): 487-494.
[4]	QU K, REN X Y, KRAATZ S. Numerical investigation of tsunami-like wave hydrodynamic characteristics and its comparison with solitary wave[J]. Applied Ocean Research, 2017, 63: 36-48. DOI URL
[5]	SATO S, OKAYASU A, YEH H, et al. Delayed survey of the 2011 Tohoku tsunami in the former exclusion zone in Minami-soma, Fukushima Prefecture[J]. Pure and Applied Geophysics, 2014, 171(12): 3229-3240. DOI URL
[6]	HARINARAYANA T, HIRATA N. Destructive earthquake and disastrous tsunami in the Indian Ocean, what next?[J]. Gondwana Research, 2005, 8(2): 246-257. DOI URL
[7]	MORI N, TAKAHASHI T. The 2011 Tohoku earthquake tsunami joint survey group. Nationwide post event survey and analysis of the 2011 Tohoku earthquake tsunami[J]. Coastal Engineering Journal, 2012, 54(1): 1250001.
[8]	QUIROGA P D, CHEUNG K F. Laboratory study of solitary-wave transformation over bed-form roughness on fringing reefs[J]. Coastal Engineering, 2013, 80: 35-48. DOI URL
[9]	YAO Y, HE F, TANG Z J, et al. A study of tsunami-like solitary wave transformation and run-up over fringing reefs[J]. Ocean Engineering, 2018, 149: 142-155. DOI URL
[10]	DE WAAL J P, VAN DER MEER J W. Wave runup and overtopping on coastal structures[C]// American Society of Civil Engineers, Coastal Engineering, 1992, 1993: 1758-1771.
[11]	HUNT A. Extreme waves, overtopping and flooding at sea defences[D]. Oxford: University of Oxford, 2003.
[12]	HSIAO S C, LIN T C. Tsunami-like solitary waves impinging and overtopping an impermeable seawall: Experiment and RANS modeling[J]. Coastal Engineering, 2010, 57(1): 1-18. DOI URL
[13]	LIN T C, HWANG K S, HSIAO S C, et al. An experimental observation of a solitary wave impingement, run-up and overtopping on a seawall[J]. Journal of Hydrodynamics, 2012, 24(1): 76-85. DOI URL
[14]	张金牛, 吴卫, 刘桦, 等. 孤立波作用下斜坡堤越浪量的实验研究[J]. 水动力学研究与进展A辑, 2014, 29(6):656-662.
	ZHANG J N, WU W, LIU H, et al. An experimental study on overtopping of solitary wave against a slope dike[J]. Journal of Hydrodynamics, 2014, 29(6): 656-662.
[15]	曾婧扬, 吴卫, 刘桦. 孤立波斜坡堤堤顶及后坡越浪流数值分析[J]. 力学季刊, 2013, 34(2):181-190.
	ZENG J Y, WU W, LIU H. Numerical analysis of overtopping flow on crest and landward slope of seadike in solitary wave[J]. Chinese Quarterly of Mechanics, 2013, 34(2): 181-190.
[16]	王键, 孙大鹏, 吴浩. 带胸墙斜坡堤越浪量的数值试验研究[J]. 海洋工程, 2018, 36(4):138-146.
	WANG J, SUN D P, WU H. Numerical study on overtopping of sloping breakwater with crown-wall[J]. The Ocean Engineering, 2018, 36(4): 138-146.
[17]	万德成, 戴世强. 孤立波与潜水台阶相互作用的数值模拟[J]. 水动力学研究与进展A辑, 1998, 13(1):95-100.
	WAN D C, DAI S Q. Numerical study of the interaction between a solitary wave and a submerged step obstacle[J]. Chinese Journal of Hydrodynamics, 1998, 13(1): 95-100.
[18]	万德成, 缪国平. 数值模拟波浪翻越直立方柱[J]. 水动力学研究与进展A辑, 1998, 13(3):363-370.
	WAN D C, MIAO G P. Numerical simulations of waves overtopping an erect quadrate column[J]. Chinese Journal of Hydrodynamics, 1998, 13(3): 363-370.
[19]	QU K, WEN B H, REN X Y, et al. Numerical investigation on hydrodynamic load of coastal bridge deck under joint action of solitary wave and wind[J]. Ocean Engineering, 2020, 217: 108037. DOI URL
[20]	WEN B H, QU K, LAN G Y, et al. Numerical study on hydrodynamic characteristics of coastal bridge deck under joint action of regular waves and wind[J]. Ocean Engineering, 2022, 245: 110450. DOI URL
[21]	GUO L, QU K, HUANG J X, et al. Numerical study of influences of onshore wind on hydrodynamic processes of solitary wave over fringing reef[J]. Journal of Marine Science and Engineering, 2022: 10: 1645.
[22]	KUNDU P K, COHEN I M, DOWLING D R. Fluid mechanics[M]. Academic Press, 2015.
[23]	ISSA R I. Solution of the implicitly discretised fluid flow equations by operator-splitting[J]. Journal of Computational Physics, 1986, 62(1): 40-65. DOI URL
[24]	FERZIGER J H, PERIĆ M. Computational methods for fluid dynamics[M]. 3rd, rev. ed. Berlin: Springer 2002.
[25]	JASAK H. Error analysis and estimation for the finite volume method with applications to fluid flows[D]. London, UK: Imperial College London, 1996.
[26]	RHIE C M, CHOW W L. Numerical study of the turbulent flow past an airfoil with trailing edge separation[J]. AIAA Journal, 1983, 21(11): 1525-1532. DOI URL
[27]	WILCOX D C. Turbulence modeling for CFD[M]. 2nd ed. La Canada, Calif.: DCW Industries, 1998.
[28]	JIANG C B, YANG Y, DENG B. Study on the nearshore evolution of regular waves under steady wind[J]. Water, 2020, 12(3): 686. DOI URL
[29]	GRILLI S T, SVENDSEN I A, SUBRAMANYA R. Breaking criterion and characteristics for solitary waves on slopes[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1997, 123(3): 102-112. DOI URL

风对孤立波海堤越浪特性影响的数值模拟研究

Numerical simulation study on influences of onshore wind on overtopping characteristics of solitary wave under coastal seawall

RichHTML

PDF

可视化

摘要/Abstract

引用本文

使用本文

图/表 28

参考文献 29

相关文章 15

编辑推荐

Metrics

[1]	吕曌, 伍志元, 蒋昌波, 张浩键, 高凯, 颜仁. 基于海气耦合模式的超强台风“山竹”数值模拟[J]. 海洋学研究, 2023, 41(4): 21-31.
[2]	张宸浩, 张明亮, 柴崇顼, 等. 基于OpenFOAM波浪—植物相互作用的数值模拟研究[J]. 海洋学研究, 2022, 40(1): 42-52.
[3]	徐浩波, 管清胜, 许明珠, 刁云云, . 蛇纹岩化作用对超慢速洋中脊拆离断层发育的影响[J]. 海洋学研究, 2021, 39(3): 21-30.
[4]	崔子健, 梁楚进, 蔺飞龙, 金魏芳, 丁涛, 王隽. 安达曼海内孤立波的潜标观测分析研究[J]. 海洋学研究, 2020, 38(4): 16-25.
[5]	周炜, 宣基亮, 黄大吉. 桑沟湾邻近海域岬角潮余流涡对及其产生机理[J]. 海洋学研究, 2020, 38(3): 10-20.
[6]	张佳丽, 张安民, 孙朝辉, 张学峰, 张亮*1. 抗差Vondrak滤波方法在内孤立波提取中的应用研究[J]. 海洋学研究, 2020, 38(1): 1-8.
[7]	伍志元, 蒋昌波, 何智勇, 陈杰, 邓斌, 谢振东. 大气-海浪耦合模式及其在理想台风模拟中的应用研究[J]. 海洋学研究, 2019, 37(2): 9-15.
[8]	苏银秋, 潘国富, 俞亮亮, 杨万康. 海湾水交换对取排水工程的响应[J]. 海洋学研究, 2018, 36(4): 76-83.
[9]	张拂坤, 邹川玲, 刘淑静, 徐显, 刘伟. 晋江海域海水淡化排海盐度场三维数值模拟[J]. 海洋学研究, 2018, 36(2): 12-18.
[10]	黄宗伟, 邓斌, 蒋昌波, 刘晓建. 环抱式港区水体交换能力数值研究——以闸坡渔港为例[J]. 海洋学研究, 2018, 36(1): 66-74.
[11]	黄潘阳, 来向华, 季有俊, 胡涛骏, 王友忠. 舟山东港新城溃堤洪水演进数值模拟[J]. 海洋学研究, 2017, 35(4): 61-68.
[12]	邹逸航, 马旭林, 姜胜, 何海伦, 郭欢. COSMIC掩星资料同化对台风“天兔”预报影响的试验[J]. 海洋学研究, 2017, 35(3): 9-19.
[13]	于凯本, 杨涛, 高健, 林广义, 孟庆健, 宗乐. 基于Flow-3D的抗拖网海床基冲刷数值模拟[J]. 海洋学研究, 2017, 35(3): 91-98.
[14]	程文龙, 潘存鸿, 吴修广. FVCOM模型关键参数的处理及其在涌潮模拟中的应用[J]. 海洋学研究, 2017, 35(1): 33-40.
[15]	徐宋昀, 许惠平, 耿明会, 关永贤. 南海东沙海域内孤立波形态研究[J]. 海洋学研究, 2016, 34(4): 1-9.